Một người nông dân mua một con bò giá 10 triệu, rồi bán đi với giá 15 triệu, sau đó mua lại giá 20 triệu rồi lại bán đi với giá 17 triệu. Người bán bò lãi bao nhiêu?

Lời giải

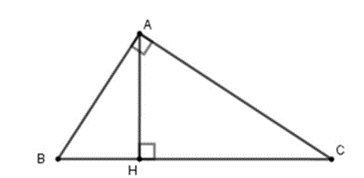
a) Xét ∆ABH và ∆CBA có:

\(\widehat {BHA} = \widehat {BAC} = 90^\circ \)

\(\widehat {ABC}\) chung.

Do đó  (g.g)

Suy ra \(\frac{{AB}}{{CB}} = \frac{{BH}}{{BA}}\) (tỉ số đồng dạng)

Do đó AB² = BH . BC.

b) Vì tam giác AHC vuông tại H nên  \(\widehat {HCA} + \widehat {HAC} = 90^\circ \)(trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Mà \(\widehat {BAH} + \widehat {HAC} = \widehat {BAC} = 90^\circ \)

Suy ra \(\widehat {BAH} = \widehat {HCA}\)

Xét ∆AHB và ∆CHA có:

\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)

\(\widehat {BAH} = \widehat {HCA}\)(chứng minh trên)

Do đó  (g.g)

Suy ra \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) (tỉ số đồng dạng)

Do đó AH² = BH . CH.

c) Ta có \[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\]

Suy ra AB . AC = AH . BC.

d) Xét ∆CAH và ∆CBA có:

\(\widehat {CHA} = \widehat {BAC} = 90^\circ \).

\(\widehat {ACB}\) chung.

Do đó  (g.g)

Suy ra \(\frac{{AC}}{{BC}} = \frac{{HC}}{{AC}}\) (tỉ số đồng dạng)

Do đó AC² = CH . BC.

Lời giải

a) Ta có:

\(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \)

= \(\overrightarrow {EA} + \overrightarrow {AB} + \overrightarrow {CD} \)

= \(\overrightarrow {EB} + \overrightarrow {CD} \)

= \(\overrightarrow {ED} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} \)

= \(\overrightarrow {ED} + \overrightarrow {CB} + (\overrightarrow {BD} + \overrightarrow {DB} )\)

= \(\overrightarrow {CB} + \overrightarrow {ED} \)

Vậy \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} \) = \(\overrightarrow {CB} + \overrightarrow {ED} \)

b) Ta có:

\(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \)

= \(\overrightarrow {AC} + \overrightarrow {CD} + \overrightarrow {CE} \)

= \(\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {CD} \)

= \(\overrightarrow {AE} + \overrightarrow {CD} \)

= \(\overrightarrow {AE} + \overrightarrow {CB} + \overrightarrow {BD} \)

= \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \)

Vậy \(\overrightarrow {AC} + \overrightarrow {CD} - \overrightarrow {EC} \) = \(\overrightarrow {A{\rm{E}}} - \overrightarrow {BD} + \overrightarrow {CB} \).