Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác.
a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC
b) Gọi H là trung điểm của BC. Kẻ đường kính IK của đường tròn (O).
Chứng minh: \(\frac{{AI}}{{AK}} = \frac{{HI}}{{HK}}\).
Cho tam giác ABC cân ở A. Gọi I là giao điểm các đường phân giác.
a) Xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp ∆BIC
b) Gọi H là trung điểm của BC. Kẻ đường kính IK của đường tròn (O).
Chứng minh: \(\frac{{AI}}{{AK}} = \frac{{HI}}{{HK}}\).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
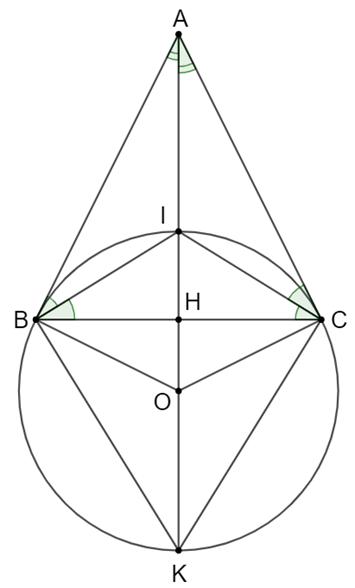
a) Vì tam giác ABC cân ở A Þ AI vừa là đường phân giác vừa là đường cao.
Do 3 điểm A, I, O thẳng hàng Þ AO ^ BC
Þ \(\widehat {OIC} + \widehat {ICB} = 90^\circ \) (1)
Vì OI = OC = R Þ ∆IOC cân tại O
Þ \(\widehat {OIC} = \widehat {ICO}\) (2)
Do CI là đường phân giác của \(\widehat C\) nên suy ra \(\widehat {ICB} = \widehat {ICA}\) (3)
Từ (1), (2) và (3) suy ra \(\widehat {ICA} + \widehat {ICO} = 90^\circ \)
\( \Rightarrow \widehat {ACO} = 90^\circ \Rightarrow AC \bot CO\)
Vậy AC là tiếp tuyến của đường tròn tâm O.
b) Do ∆CIK nội tiếp đường tròn (O)
\( \Rightarrow \widehat {ICK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Þ CK ^ CI
Mà CI là đường phân giác góc trong \(\widehat C\)
Þ CK là đường phân giác góc ngoài của \(\widehat {ACB}\)
Nên theo tích chất đường phân giác ta có:
\(\frac{{AI}}{{AK}} = \frac{{HI}}{{HK}}\) (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
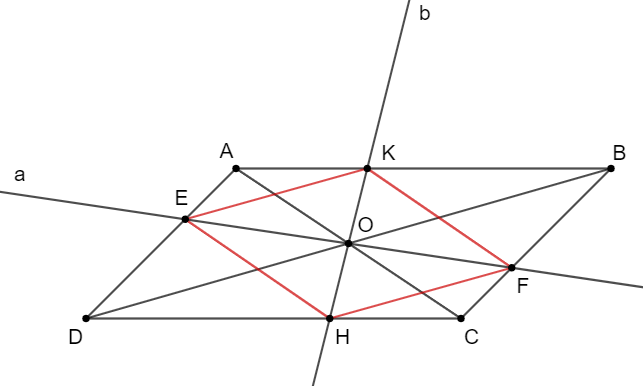
Do ABCD là hình bình hành nên ta có:
+) \(AB\;{\rm{//}}\;{\rm{CD}} \Rightarrow \widehat {ABD} = \widehat {BDC}\) (Hai góc ở vị trí so le trong).
\( \Rightarrow \widehat {KBO} = \widehat {HDO}\).
+) \(AD\;{\rm{//}}\;B{\rm{C}} \Rightarrow \widehat {DAC} = \widehat {ACB}\) (Hai góc ở vị trí so le trong).
\( \Rightarrow \widehat {EAO} = \widehat {FCO}\).
Xét ∆KOB và ∆HOD có:
\(\widehat {KBO} = \widehat {HDO}\) (cmt)
OB = OD (gt)
\(\widehat {KOB} = \widehat {HOD}\) (Hai góc đối đỉnh)
Þ ∆KOB = ∆HOD (g.c.g)
Þ OK = OH (Hai cạnh tương ứng bằng nhau) (1)
Xét ∆EOA và ∆FOC có:
\(\widehat {EAO} = \widehat {FCO}\) (cmt)
OA = OC (gt)
\(\widehat {EOA} = \widehat {FOC}\) (Hai góc đối đỉnh)
Þ ∆EOA = ∆FOC (g.c.g)
Þ OE = OF (Hai cạnh tương ứng bằng nhau) (2)
Từ (1) và (2) ta có tứ giác EKFH có hai cặp cạnh đối thỏa mãn OK = OH và OE = OF.
Suy ra EKFH là hình bình hành.
Lời giải
Lời giải
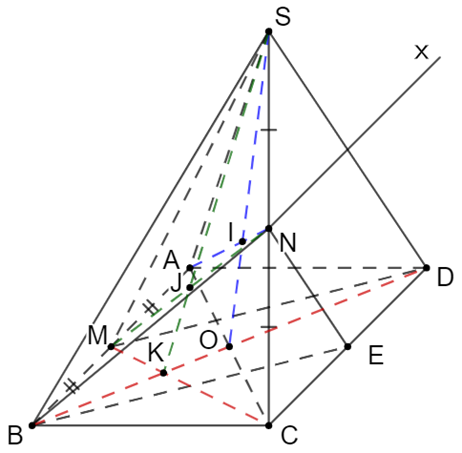
a) N là điểm chung của (ABN) và (SCD).
Mà AB // CD Þ (ABN) ∩ (SCD) = Nx // CD // AB.
b) Gọi E là trung điểm của CD
\( \Rightarrow DE = MB = \frac{1}{2}CD = \frac{1}{2}AB\).
Xét tam giác CSD có \(\frac{{EC}}{{CD}} = \frac{{CN}}{{SC}} = \frac{1}{2}\).
Áp dụng định lý Ta-lét đảo suy ra: EN // SD (1)
Ta thấy BM // DE và BM = DE suy ra DMBE là hình bình hành.
Þ BE // DM (2)
Từ (1) và (2) Þ (BNE) // (SDM)
Þ BN // (SDM)
c) Gọi O là tâm của hình bình hành ABCD.
Ta có O Î (SBD) Þ SO Ì (SBD)
Þ I = SO Ç AN là điểm cần tìm.
Gọi K là giao điểm của MC và BD
Þ K Î (SBD) Þ SK Ì (SBD)
Þ J = SK Ç MN là điểm cần tìm.
d) Xét tam giác SAC có I là giao điểm của hai đường trung tuyến là SO và AN nên I là trọng tâm của tam giác SAC
\( \Rightarrow \frac{{AI}}{{AN}} = \frac{2}{3}\)
Do MB // CD nên theo định lí Ta-lét ta có: \(\frac{{MB}}{{CD}} = \frac{{MK}}{{KC}} = \frac{1}{2} \Rightarrow \frac{{MK}}{{MC}} = \frac{1}{3}\).
Xét tam giác MSC có:
\(\frac{{MC}}{{MK}} + \frac{{MS}}{{MS}} = 2\frac{{MN}}{{MJ}}\)
\( \Rightarrow 3 + 1 = 2 \cdot \frac{{MN}}{{MJ}} \Rightarrow \frac{{MJ}}{{MN}} = \frac{1}{2}\)
Xét tam giác BNA có:
\(\frac{{BN}}{{BN}} + \frac{{BA}}{{BM}} = 2\frac{{BI}}{{BJ}}\)
\( \Rightarrow 1 + 2 = 2 \cdot \frac{{BI}}{{BJ}} \Rightarrow \frac{{IB}}{{BJ}} = \frac{3}{2} \Rightarrow \frac{{IB}}{{IJ}} = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.