Câu hỏi:

12/07/2024 3,867

Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.

a) CM: CD = AC + BD.

b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. CM: AF.BC = KE.EB.

c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.

d) EA cắt CF tại M. EB cắt DF tại N. CM: M, I, N thẳng hàng.

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

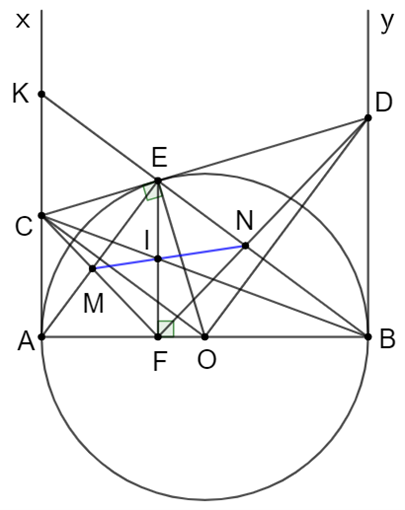
Media VietJack

a) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:

• Ax và CD là 2 tiếp tuyến cắt nhau tại C Þ CA = CE;

• By và CD là 2 tiếp tuyến cắt nhau tại D Þ DB = DE.

Suy ra: AC + BD = CE + DE = CD (đpcm)

b) ΔAEB nội tiếp đường tròn đường kính AB

Þ ΔAEB vuông tại E mà EF là đường cao

Áp dụng hệ thức lượng trong tam giác vuông, ta được: AF.AB = AE² (1)

ΔBAK vuông tại A có AE là đường cao

Áp dụng hệ thức lượng trong tam giác vuông, ta được: KE.EB = AE² (2)

Từ (1) và (2) suy ra: AF.AB = KE.EB (đpcm)

c) Ax // By (cùng ^ AB), theo định lí Ta-lét ta có: \(\frac{{CE}}{{ED}} = \frac{{CI}}{{IB}} = \frac{{AF}}{{FB}}\).

Mà CE = CA và ED = BD

Þ \(\frac{{AF}}{{FB}} = \frac{{CA}}{{BD}}\)

Lại có \(\widehat {CAF} = \widehat {FBD} = 90^\circ \)

Do đó ΔAFC ᔕ ΔBFD (c.g.c) (đpcm)

d) Ta có: CA = CE; OA = OE Þ OC là đường trung trực của AE

Mà AE ^ EB Þ OC // EB hay OC // BK

Lại có O là trung điểm của BC

Þ C là trung điểm của AK Þ AC = CK

EF // AK Þ \(\frac{{IE}}{{CK}} = \frac{{BI}}{{BC}} = \frac{{IF}}{{AC}}\)

Mà AC = CK Þ IE = IF

Gọi P = IM Ç Ax; Q = IN Ç By

Ta có: CP // IF Þ \(\frac{{CP}}{{IF}} = \frac{{MP}}{{MI}}\)

PA // IE Þ \(\frac{{MP}}{{MI}} = \frac{{AP}}{{IE}}\)

Mà IE = IF Þ CP = MP Þ P là trung điểm của AC.

Chứng minh tương tự ta có Q là trung điểm của BD.

IE // BD Þ \(\frac{{CI}}{{IB}} = \frac{{CE}}{{ED}} = \frac{{CA}}{{BD}} = \frac{{2CP}}{{2QB}} = \frac{{CP}}{{QB}}\)

và \(\widehat {PCI} = \widehat {QBI}\)

Þ ΔPCI ᔕ ΔQBI (c.g.c)

\( \Rightarrow \widehat {QIB} + \widehat {PIB} = \widehat {PIC} + \widehat {PIB} = 180^\circ \)

Þ P, I, Q thẳng hàng Þ M, I, N thẳng hàng (đpcm)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. Qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.

Xem đáp án

Lời giải

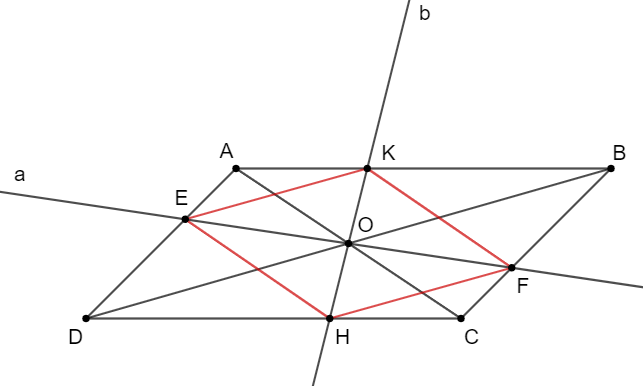
Media VietJack

Do ABCD là hình bình hành nên ta có:

+) \(AB\;{\rm{//}}\;{\rm{CD}} \Rightarrow \widehat {ABD} = \widehat {BDC}\) (Hai góc ở vị trí so le trong).

\( \Rightarrow \widehat {KBO} = \widehat {HDO}\).

+) \(AD\;{\rm{//}}\;B{\rm{C}} \Rightarrow \widehat {DAC} = \widehat {ACB}\) (Hai góc ở vị trí so le trong).

\( \Rightarrow \widehat {EAO} = \widehat {FCO}\).

Xét ∆KOB và ∆HOD có:

\(\widehat {KBO} = \widehat {HDO}\) (cmt)

OB = OD (gt)

\(\widehat {KOB} = \widehat {HOD}\) (Hai góc đối đỉnh)

Þ ∆KOB = ∆HOD (g.c.g)

Þ OK = OH (Hai cạnh tương ứng bằng nhau) (1)

Xét ∆EOA và ∆FOC có:

\(\widehat {EAO} = \widehat {FCO}\) (cmt)

OA = OC (gt)

\(\widehat {EOA} = \widehat {FOC}\) (Hai góc đối đỉnh)

Þ ∆EOA = ∆FOC (g.c.g)

Þ OE = OF (Hai cạnh tương ứng bằng nhau) (2)

Từ (1) và (2) ta có tứ giác EKFH có hai cặp cạnh đối thỏa mãn OK = OH và OE = OF.

Suy ra EKFH là hình bình hành.

Câu 2

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC.
a) Tìm giao tuyến của hai mặt phẳng (ABN) và (SCD).
b) Chứng minh đường thẳng BN song song với mặt phẳng (SDM).
c) Xác định các điểm I, J lần lượt là giao điểm của đường thẳng AN và đường thẳng MN với mặt phẳng (SBD).
d) Tính tỉ số \(\frac{{IB}}{{IJ}}\).

Xem đáp án

Lời giải

Lời giải

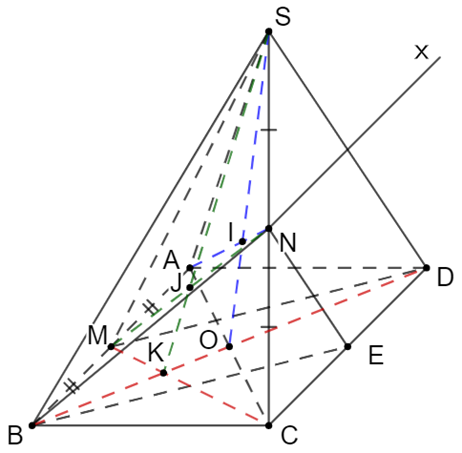
Media VietJack

a) N là điểm chung của (ABN) và (SCD).

Mà AB // CD Þ (ABN) ∩ (SCD) = Nx // CD // AB.

b) Gọi E là trung điểm của CD

\( \Rightarrow DE = MB = \frac{1}{2}CD = \frac{1}{2}AB\).

Xét tam giác CSD có \(\frac{{EC}}{{CD}} = \frac{{CN}}{{SC}} = \frac{1}{2}\).

Áp dụng định lý Ta-lét đảo suy ra: EN // SD (1)

Ta thấy BM // DE và BM = DE suy ra DMBE là hình bình hành.

Þ BE // DM (2)

Từ (1) và (2) Þ (BNE) // (SDM)

Þ BN // (SDM)

c) Gọi O là tâm của hình bình hành ABCD.

Ta có O Î (SBD) Þ SO Ì (SBD)

Þ I = SO Ç AN là điểm cần tìm.

Gọi K là giao điểm của MC và BD

Þ K Î (SBD) Þ SK Ì (SBD)

Þ J = SK Ç MN là điểm cần tìm.

d) Xét tam giác SAC có I là giao điểm của hai đường trung tuyến là SO và AN nên I là trọng tâm của tam giác SAC

\( \Rightarrow \frac{{AI}}{{AN}} = \frac{2}{3}\)

Do MB // CD nên theo định lí Ta-lét ta có: \(\frac{{MB}}{{CD}} = \frac{{MK}}{{KC}} = \frac{1}{2} \Rightarrow \frac{{MK}}{{MC}} = \frac{1}{3}\).

Xét tam giác MSC có:

\(\frac{{MC}}{{MK}} + \frac{{MS}}{{MS}} = 2\frac{{MN}}{{MJ}}\)

\( \Rightarrow 3 + 1 = 2 \cdot \frac{{MN}}{{MJ}} \Rightarrow \frac{{MJ}}{{MN}} = \frac{1}{2}\)

Xét tam giác BNA có:

\(\frac{{BN}}{{BN}} + \frac{{BA}}{{BM}} = 2\frac{{BI}}{{BJ}}\)

\( \Rightarrow 1 + 2 = 2 \cdot \frac{{BI}}{{BJ}} \Rightarrow \frac{{IB}}{{BJ}} = \frac{3}{2} \Rightarrow \frac{{IB}}{{IJ}} = 3\).

Câu 3