Hai con đường lớn a và b cắt nhau tạo thành một góc. Bên trong góc đó có một điểm dân cư O. Phải mở một con đường thẳng đi qua O như thế nào để theo con đường đó, hai đoạn đường từ điểm O đến con đường a và b bằng nhau (các con đường đều là đường thẳng) (H.3.27)?

Hai con đường lớn a và b cắt nhau tạo thành một góc. Bên trong góc đó có một điểm dân cư O. Phải mở một con đường thẳng đi qua O như thế nào để theo con đường đó, hai đoạn đường từ điểm O đến con đường a và b bằng nhau (các con đường đều là đường thẳng) (H.3.27)?

Câu hỏi trong đề: Giải SGK Toán 8 KNTT Bài 12. Hình bình hành có đáp án !!
Quảng cáo
Trả lời:
Sau bài học này ta giải quyết được bài toán như sau:
Gọi điểm giao nhau giữa hai đường thẳng a và b là điểm O
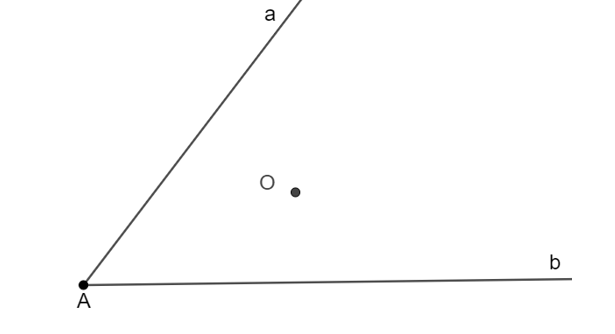
- Vẽ tia Ax đi qua điểm O. Trên tia Ax lấy điểm B sao cho OA = OB.
- Qua B vẽ tia By // Ab; Bz // Aa cắt hai tia Aa và Bb lần lượt tại hai điểm C và D
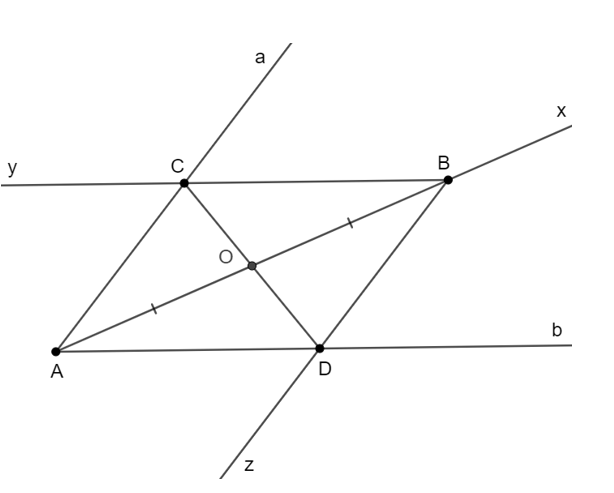
Khi đó, tứ giác ACBD là hình bình hành (vì AC // BD; AD // BC) có O là trung điểm AB nên O là trung điểm của CD.
Hai đoạn đường từ điểm O đến con đường a và b bằng nhau, tức là OC = OD.
Vậy con đường cần mở đường thẳng đi qua hai điểm C và D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
Xét tứ giác BEDF có:
BE = DF (chứng minh trên);
BE // DF (vì AB // CD)
Do đó tứ giác BEDF là hình bình hành.
Suy ra BF = DE (đpcm).
Lời giải
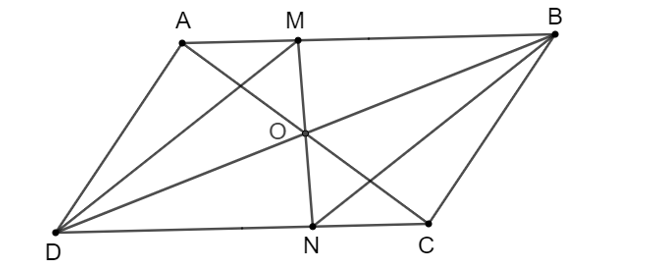
Vì ABCD là hình bình hành nên ta có:
• Hai đường chéo AC và BD cắt nhau tại O nên OA = OC, OB = OD.
• AB // CD nên AM // CN suy ra (hai góc so le trong).
Xét ∆OAM và ∆OCN có:
(chứng minh trên)
OA = OC (chứng minh trên)
(hai góc đối đỉnh)
Do đó ∆OAM = ∆OCN (g.c.g).
Suy ra AM = CN (hai cạnh tương ứng)
Mặt khác, AB = CD (chứng minh trên); AB = AM + BM; CD = CN + DN.
Suy ra BM = DN.
Xét tứ giác MBND có:
• BM // DN (vì AB // CD)
• BM = DN (chứng minh trên)
Do đó, tứ giác MBND là hình bình hành.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.