Câu hỏi:
01/04/2023 2,857Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB đều và nằm trong một mặt phẳng vuông góc với đáy. Gọi H, K lần lượt là trung điểm của các cạnh AB và AD. Tính sin của góc tạo bởi giữa đường thẳng SA và mặt phẳng (SHK).
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Đáp án đúng là: B.
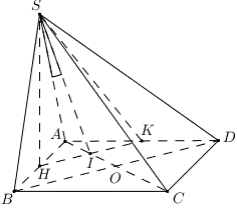
Theo đề bài ∆SAB đều nên SH ⊥ AB suy ra SH ⊥ (ABCD).
Gọi I = AC ∩ HK.
Do ABCD là hình vuông nên AC ⊥ BD.
Mà HK // BD (H là đường trung bình của \(\Delta ABD\) nên AC ⊥ HK.
Do đó AI ⊥ BD.
Ta có: \(\left\{ \begin{array}{l}AI \bot HK\\AI \bot SH(SH \bot (ABCD))\end{array} \right.\)\( \Rightarrow AI \bot (SHK)\).
Suy ra SI là hình chiếu của SA lên (SHK).
Gọi = AC ∩ BD, áp dụng định lí Ta-lét ta có:
\(\frac{{AI}}{{OA}} = \frac{{AH}}{{AB}} = \frac{1}{2} \Rightarrow AI = \frac{1}{2}OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{4}\).
Xét ∆SIA vuông tại I ta có: \(\widehat {ISA} = \frac{{AI}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{4}}}{a} = \frac{{\sqrt 2 }}{4}\).
Vậy \[\sin \widehat {\left( {SA;\,\,\left( {SHK} \right)} \right)} = \frac{{\sqrt 2 }}{4}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Hàm số y = ln(x2 – 2mx + m) có tập xác định D = ℝ khi và chỉ khi
x2 – 2mx + 4 > 0 với mọi x ∈ ℝ.
\( \Rightarrow \left\{ \begin{array}{l}\Delta ' < 0\forall x\\1 > 0\end{array} \right.\)
\( \Leftrightarrow {m^2} - 4 < 0 \Leftrightarrow - 2 < m < 2\)
Vậy \( - 2 < m < 2\) thỏa mãn yêu cầu bài toán.
Lời giải
Lời giải
Đáp án đúng là A.
Ta có: \(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{CA}}{{\sin B}}\)
\( \Rightarrow \left\{ \begin{array}{l}BC = \frac{{\sin A}}{{\sin C}}\,.\,AB\\CA = \frac{{\sin B}}{{\sin C}}\,.\,AB\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}BC = 2.6 = 12\\CA = \frac{4}{3}.6 = 8\end{array} \right.\).
Vậy chu vi tam giác ABC là: AB + BC +CA = 6 + 12 + 8 = 26.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận