Tìm nghiệm âm lớn nhất của phương trình \(\sin x + \cos x = 1 - \frac{1}{2}\sin 2x\).

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương trình \(\sin x + \cos x = 1 - \frac{1}{2}\sin 2x\) có nghĩa\(\forall \)x ∈ ℝ ⟺ D = ℝ.

Ta có: \(\sin x + \cos x = 1 - \frac{1}{2}\sin 2x\)⟺ sinx + cosx +sinxcosx – 1 = 0 (1)

Đặt t = sinx +cosx, \(\left( {\left| t \right| \le \sqrt 2 } \right)\). Ta có sinxcosx = \(\frac{{{t^2} - 1}}{2}\)

⇒ (1) ⟺ \(t + \frac{{{t^2} - 1}}{2} - 1 = 0 \Leftrightarrow {t^2} + 2t - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1}\\{t = - 3}\end{array}} \right.\)

Do \(\left| t \right| \le \sqrt 2 \)nên t = 1

Với t = 1, ta có t = sinx + cosx = \(\sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = 1 \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2} = \sin \frac{\pi }{4}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \Leftrightarrow x = k2\pi }\\{x + \frac{\pi }{4} = \frac{{3\pi }}{4} + k2\pi \Leftrightarrow x = \frac{\pi }{2} + k2\pi }\end{array}} \right.,k \in \mathbb{Z}\)

Vậy nghiệm âm lớn nhất của phương trình là \(x = - \frac{{3\pi }}{2}\)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho α là góc tù và sinα – cosα = \(\frac{4}{5}\). Giá trị của M = sinα – 2cosα là ?

Xem đáp án

Lời giải

Vì α là góc tù nên \(\sin \alpha = \sqrt {1 - {{\cos }^2}\alpha } \).

Do đó, sin α – cos α = \(\frac{4}{5}\)

\( \Leftrightarrow \sqrt {1 - {{\cos }^2}\alpha } - \cos \alpha = \frac{4}{5}\)

\( \Leftrightarrow \sqrt {1 - {{\cos }^2}\alpha } = \cos \alpha + \frac{4}{5} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{1 - {{\cos }^2}\alpha = {{\left( {\cos \alpha + \frac{4}{5}} \right)}^2}}\\{\cos \alpha \ge - \frac{4}{5}}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{50{{\cos }^2}\alpha + 40\cos \alpha - 9 = 0}\\{\cos \alpha \ge - \frac{4}{5}}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{\cos \alpha = \frac{{ - 4 + \sqrt {34} }}{{10}}}\\{\cos \alpha = \frac{{ - 4 - \sqrt {34} }}{{10}}}\end{array}} \right.}\\{\cos \alpha \ge - \frac{4}{5}}\end{array}} \right. \Leftrightarrow \cos \alpha = - \frac{{4 + \sqrt {34} }}{{10}}\) (do α tù)

⇒ m = sin α – 2cos α = (sin α – cos α) – cos α = \(\frac{4}{5} + \frac{{4 + \sqrt {34} }}{{10}} = \frac{{12 + \sqrt {34} }}{{10}}\).

Câu 2

Cho (O; R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A vẽ 2 tiếp tuyến AB, AC của đường tròn (O) (B, C là tiếp điểm). Vẽ dây BE của đường tròn (O) song song với AC; AE cắt (O) tại D khác E; BD cắt AC tại S. Gọi M là trung điểm của đoạn DE.

a. Chứng minh 5 điểm A, B, C, O, M cùng thuộc 1 đường tròn

b. Chứng minh \(S{C^2}\)= SB.SD

c. 2 đường thẳng DE và BC cắt nhau tại V; đường thẳng SV cắt BE tại H. Chứng minh 3 điểm H, O, C thẳng hàng.

Xem đáp án

Lời giải

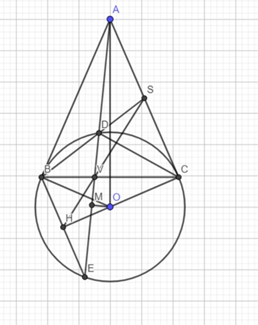
Cho (O; R) và điểm A nằm ngoài đường tròn với OA > 2R. Từ A vẽ 2 tiếp tuyến (ảnh 1)

a. Ta có AB, AC là tiếp tuyến của (O) ⇒ AB ⊥ BO, AC ⊥ CO

M là trung điểm DE ⇒ OM ⊥ DE

\( \Rightarrow \widehat {ABO} = \widehat {AMO} = \widehat {ACO} = 90^\circ \)

⇒ A, B, M, O, C ∈ đường tròn đường kính AO

b. Xét ∆SCD, ∆SCB có:

Chung \(\widehat S\)

\(\widehat {SCD} = \widehat {SBC}\)vì SC là tiếp tuyến của (O)

⇒ ∆SAD \(\# \) ∆SBC (g.g)

\( \Rightarrow \frac{{SC}}{{SB}} = \frac{{SD}}{{SC}} \Rightarrow S{C^2} = SB.SD\)

c. Xét ∆SAD, ∆SAB có:

Chung \(\widehat S\)

\(\widehat {SAD} = \widehat {DEB} = \widehat {ABS}\) vì AB là tiếp tuyến của (O) và BE //AC

⇒ ∆SAD \(\# \) ∆SBA (g.g)

\( \Rightarrow \frac{{SA}}{{SB}} = \frac{{SD}}{{SA}} \Rightarrow S{A^2} = SB.SD \Rightarrow S{A^2} = S{C^2} \Rightarrow SA = SC\)

Lại có AC // BE

\( \Rightarrow \frac{{BH}}{{SC}} = \frac{{VH}}{{VS}} = \frac{{HE}}{{AS}} \Rightarrow BH = HE\)

H là trung điểm BE ⇒ OH ⊥ BE (1)

Ta có BE // AC

\( \Rightarrow \widehat {EBC} = \widehat {ACB} = \widehat {CEB}\) ⇒ ∆CBE cân tại C ⇒ CO ⊥ BE (2)

Từ (1), (2) ⇒ C, O, H thẳng hàng.

Câu 3