Cho tứ diện S.ABC. Gọi O là điểm thuộc miền trong của tam giác ABC. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh SA, SC sao cho MN không song song với AC. Tìm thiết diện do (MNO) cắt tứ diện S.ABC.
Cho tứ diện S.ABC. Gọi O là điểm thuộc miền trong của tam giác ABC. Gọi M, N lần lượt là hai điểm nằm trên hai cạnh SA, SC sao cho MN không song song với AC. Tìm thiết diện do (MNO) cắt tứ diện S.ABC.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
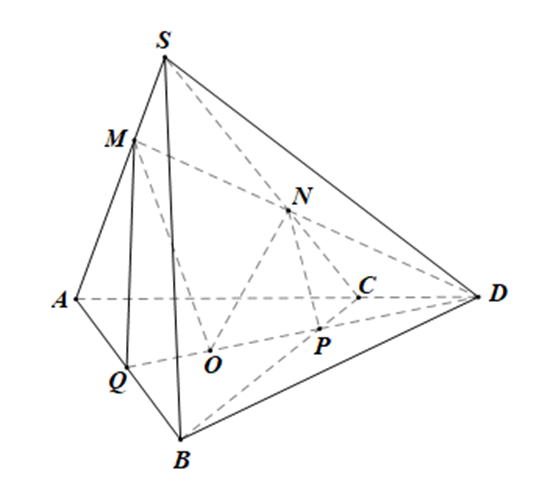
• (OMN) ∩ (SAC) = MN;
• Trong mp(SAC), gọi D = MN ∩ AC.
Trong mp(ABC), gọi P = BC ∩ OD.
Khi đó P ∈ OD ⊂ (OMN) và P ∈ (SBC), suy ra P = (OMN) ∩ (SBC)
Mà N = (OMN) ∩ (SBC), suy ra (OMN) ∩ (SBC) = NP.
• Do P ∈ BC, BC ⊂ (ABC) nên P ∈ (ABC)
Suy ra P = (OMN) ∩ (ABC)
Lại có O = (OMN) ∩ (ABC)
Suy ra (OMN) ∩ (ABC) = OP.
• Trong mp(ABC), gọi Q = OP ∩ AB.
Khi đó Q ∈ (OMN) và Q ∈ (ABC) nên Q = (OMN) ∩ (ABC)
Lại có M ∈ (OMN) và M ∈ (ABC) nên M = (OMN) ∩ (ABC)
Suy ra (OMN) ∩ (ABC) = QM.
Vậy thiết diện do (MNO) cắt tứ diện S.ABC là (MNPQ).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
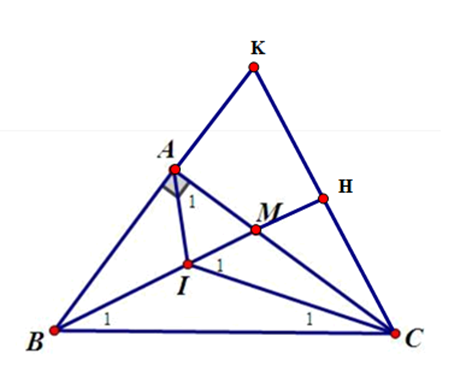
a) Vì tam giác ABC vuông tại A nên \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Vì AI là phân giác của góc BAC nên \(\widehat {{A_1}} = \frac{{\widehat {BAC}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \)
Vì BI là phân giác của góc ABC nên \(\widehat {{B_1}} = \frac{{\widehat {ABC}}}{2}\)
Vì CI là phân giác của góc ACB nên \(\widehat {{C_1}} = \frac{{\widehat {ACB}}}{2}\)
Gọi giao điểm của BI và AC là M.
Vì \(\widehat {{I_1}}\) là góc ngoài của tam giác BIC
Nên \(\widehat {{I_1}} = \widehat {{B_1}} + \widehat {{C_1}} = \frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = \frac{{\widehat {ABC} + \widehat {ACB}}}{2} = \frac{{90^\circ }}{2} = 45^\circ \)
Xét DICM và DACI có
\(\widehat {{A_1}} = \widehat {{I_1}}\left( { = 45^\circ } \right)\);
\(\widehat {IC{\rm{A}}}\) là góc chung
Do đó (g.g)
Suy ra \(\frac{{IC}}{{AC}} = \frac{{CM}}{{CI}}\) (tỉ số đồng dạng)
Hay CI2 = CM . AC, mà IC = 6 nên CM . AC = 36
Suy ra \(CM = \frac{{36}}{{AC}}\).
Do BM là tia phân giác của \(\widehat {ABC}\) nên ta có
\(\frac{{CB}}{{AB}} = \frac{{CM}}{{MA}} \Leftrightarrow \frac{{BC}}{{BA + BC}} = \frac{{CM}}{{MA + CM}} \Leftrightarrow \frac{{BC}}{{5 + BC}} = \frac{{CM}}{{AC}}\)
Mà \(CM = \frac{{36}}{{AC}}\)
Suy ra \(\frac{{36}}{{A{C^2}}} = \frac{{BC}}{{BC + 5}} \Leftrightarrow \frac{{36}}{{B{C^2} - A{B^2}}} = \frac{{BC}}{{BC + 5}} \Leftrightarrow \frac{{36}}{{B{C^2} - 25}} = \frac{{BC}}{{BC + 5}}\)
\( \Leftrightarrow \frac{{36}}{{B{C^2} - 25}} = \frac{{BC\left( {BC - 5} \right)}}{{B{C^2} - 25}}\)
Suy ra BC(BC – 5) = 36
Hay BC2 – 5BC – 36 = 0
Suy ra BC = 9 (do BC > 0).
b) Kẻ CH ⊥ BI và CH cắt BA tại K.
Xét tam giác BCK có BH vừa là tia phân giác vừa là đường cao
Suy ra tam giác BCK cân tại B
Do đó BH là trung tuyến và BK = BC
Hay \[CH = HK = \frac{1}{2}CK\]
Đặt BC = x
Ta có AK = BK – AB = BC – AB = x – AB
Ta có: \(\widehat {ABM} = \widehat {HCM}\) (cùng phụ với \(\widehat {BKC}\))
Mà \(\widehat {ABM} = \frac{1}{2}\widehat {ABC}\) nên \(\widehat {HCM} = \frac{1}{2}\widehat {ABC}\)
Ta có \(\widehat {HCI} = \widehat {HCM} + \widehat {MCI} = \frac{1}{2}\widehat {ABC} + \frac{1}{2}\widehat {ACB} = \frac{1}{2}.90^\circ = 45^\circ \)
Xét tam giác ICH vuông ở H có
\(\widehat {HIC} + \widehat {HCI} = 90^\circ \) (trong một tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {HCI} = 45^\circ \) nên \(\widehat {HIC} = 45^\circ \)
Suy ra \(\widehat {HCI} = \widehat {HIC}\)
Do đó tam giác HIC vuông ở H, nên HI = HC
Xét tam giác ICH vuông ở H có
IC2 = HI2 + HC2 (định lí Pytago)
Hay 10 = 2HI2 (do \(IC = \sqrt {10} \))
Suy ra \[HI = HC = \sqrt 5 \]
Ta có \[BH = BI + IH = \sqrt 5 + \sqrt 5 = 2\sqrt 5 \];
\[CK = 2CH = 2\sqrt 5 \]
Xét tam giác BCH vuông ở H có
BC2 = HB2 + HC2 (định lí Pytago)
Hay BC2 = 20 + 5
Suy ra BC = 5.
Xét tam giác BCA vuông ở A có
BC2 = AB2 + AC2 (định lí Pytago)
Hay 52 = AB2 + AC2 = 25
Xét tam giác AKC vuông ở A có
KC2 = AK2 + AC2 (định lí Pytago)
⇔ 20 = (BC – AB)2 + AC2
⇔ 20 = (5 – AB)2 + AC2
⇔ 20 = 25 – 10AB + AB2 + AC2
⇔ 20 = 25 – 10AB + 25
⇔ AB = 3
Khi đó \(AC = \sqrt {{5^2} - {3^2}} = 4\)
Vậy AB = 3, AC = 4.
Lời giải
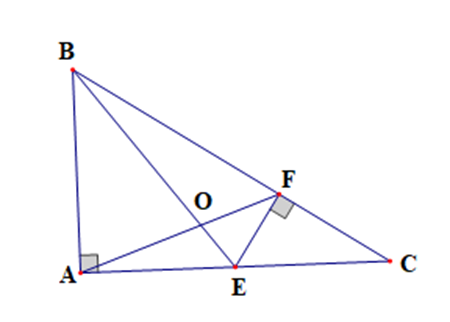
a) Xét tam giác CEF vuông ở F có \(\cos C = \frac{{CF}}{{CE}}\)
Xét tam giác CEF và tam giác CBA có
\(\widehat C\) là góc chung;
\(\widehat {BAC} = \widehat {{\rm{EF}}C} = 90^\circ \)
Suy ra (g.g)
Do đó \(\frac{{CF}}{{CE}} = \frac{{CA}}{{CB}}\)
Xét tam giác AFC và tam giác BEC có
\(\widehat C\) là góc chung;
\(\frac{{CF}}{{CE}} = \frac{{CA}}{{CB}}\) (chứng minh trên)
Suy ra (g.g)
Do đó \(\frac{{CF}}{{CE}} = \frac{{FA}}{{BE}}\)
Mà cosC = \(\frac{{CF}}{{CE}}\)
Suy ra AF = BE . cosC.
b) Vì tam giác ABC vuông tại A
Suy ra AB = BC . sinC = 10 . 0,6 = 6.
Xét tam giác ABC vuông tại A, theo định lí Pytago có
BC2 = AB2 + AC2
Suy ra \(AC = \sqrt {B{C^2} - A{B^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)
Mà E là trung điểm AC nên AE = EC = 4
Vì tam giác FEC vuông tại F
Suy ra FE = EC . sinC = 4 . 0,6 = 2,4
Xét tam giác FEC vuông tại F, theo định lí Pytago có
EC2 = FE2 + FC2
Suy ra \(FC = \sqrt {E{C^2} - F{{\rm{E}}^2}} = \sqrt {{4^2} - 2,{4^2}} = 3,2\)
Khi đó BF = BC – FC = 10 – 3,2 = 6,8
Ta có SABFE = SABE + SBFE
\( = \frac{1}{2}AB.AE + \frac{1}{2}BF.FE\)
\( = \frac{1}{2}.6.4 + \frac{1}{2}.6,8.2,4 = 20,16\left( {c{m^2}} \right)\)
c) Ta có \(\frac{{CF}}{{CE}} = \frac{{FA}}{{BE}} = \frac{{3,2}}{4}\)
Suy ra AF = 0,8BE
Vì tam giác ABE vuông tại A nên
BE2 = AB2 + AE2
Hay BE2 = 62 + 42
suy ra \(BE = \sqrt {52} \)
Ta có \[{S_{ABFE}} = \frac{1}{2}AF.BE.\sin \widehat {AOB}\]
\( \Leftrightarrow 20,16 = \frac{1}{2}.0,8.\sqrt {52} .\sqrt {52} .\sin \widehat {AOB}\)
\( \Leftrightarrow \sin \widehat {AOB} = \frac{{20,16}}{{20,8}} = \frac{{63}}{{65}}\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.