Giải phương trình: \[cos7x.cos5x--\sqrt 3 sin2x = 1--sin7x.sin5x\].

Lời giải

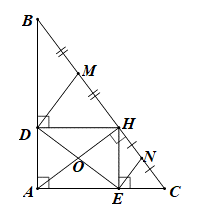
a) Xét ΔABH vuông tại H có HD ⊥ AB

Suy ra AH² = AD . AB (hệ thức lượng trong tam giác vuông)

Xét ΔAEH vuông tại H có HE ⊥ AC

Suy ra AH² = AE . AC (hệ thức lượng trong tam giác vuông)

Mà AH² = AD . AB (chứng minh trên)

Suy ra AD . AB = AE . AC

b) Vì ΔABC vuông tại A nên AB² + AC² = BC² (định lý Pytago)

Xét ΔABC vuông tại A có AH ⊥ BC

Suy ra AB² = BH . BC (hệ thức lượng trong tam giác vuông)

⇔ AB² . BC = BH . BC²

\( \Leftrightarrow \frac{{BH}}{{BC}} = \frac{{A{B^2}}}{{B{C^2}}}\)

\( \Leftrightarrow \frac{{BH}}{{BC - BH}} = \frac{{A{B^2}}}{{B{C^2} - A{B^2}}}\)

\( \Leftrightarrow \frac{{BH}}{{HC}} = \frac{{A{B^2}}}{{A{C^2}}} = {\left( {\frac{{AB}}{{AC}}} \right)^2}\)

c) Xét ΔABC vuông tại A có AH ⊥ BC

Suy ra AH² = BH . HC (hệ thức lượng trong tam giác vuông)

Hay AH² = 4 . 9 = 36

Suy ra AH = 6

Xét tứ giác ADHE có \(\widehat {DAE} = \widehat {A{\rm{D}}H} = \widehat {A{\rm{E}}H} = 90^\circ \)

Suy ra ADHE là hình chữ nhật

Mà AH, DE là hai đường chéo

Suy ra DE = AH = 6 (cm)

Vì ΔABH vuông tại H nên HB² + AH² = BA² (định lý Pytago)

Hay 4² + 6² = AB²

Suy ra \(AB = 2\sqrt {13} \)

Xét ΔABH vuông tại H có HD ⊥ AB

Suy ra AH² = AD . AB (hệ thức lượng trong tam giác vuông)

Hay \({6^2} = A{\rm{D }}.{\rm{ }}2\sqrt {13} \)

Suy ra \(A{\rm{D = }}\frac{{18}}{{\sqrt {13} }}\)

Xét tam giác ADE vuông tại A có

\({\rm{cos}}\widehat {A{\rm{D}}E} = \frac{{A{\rm{D}}}}{{DE}} = \frac{{18}}{{6\sqrt {13} }} = \frac{3}{{\sqrt {13} }}\)

Suy ra \(\widehat {A{\rm{D}}E} \approx 33^\circ \).

d) Vì ra ADHE là hình chữ nhật có AH, DE là hai đường chéo

Suy ra AH cắt DE tại trung điểm O của mỗi đường

Mà AH = DE

Do đó OH = OD

Suy ra tam giác OHD cân tại O

Suy ra \(\widehat {OH{\rm{D}}} = \widehat {O{\rm{D}}H}\)

Xét ΔHBD vuông tại D có DM là đường trung tuyến ứng với cạnh huyền

Suy ra \(DM = MH = \frac{1}{2}BH = \frac{1}{2}.4 = 2\)

Do đó ΔDMH cân tại M

Suy ra \(\widehat {MDH} = \widehat {MH{\rm{D}}}\)

Mà \(\widehat {DHA} + \widehat {MH{\rm{D}}} = \widehat {AHB} = 90^\circ \) và \(\widehat {AH{\rm{D}}} = \widehat {{\rm{ED}}H}\)(chứng minh trên)

Suy ra \(\widehat {H{\rm{D}}E} + \widehat {M{\rm{DH}}} = \widehat {M{\rm{D}}E} = 90^\circ \)

Hay MD ⊥ DE.

Chứng minh tương tự ta có \(EN = \frac{{CH}}{2} = \frac{9}{2} = 4,5\)

và \(\widehat {DEH} + \widehat {HEN} = \widehat {AHE} + \widehat {{\rm{EHN}}} = \widehat {AHC} = 90^\circ \)

Hay \(\widehat {DEN} = 90^\circ \)

Suy ra EN ⊥ DE

Mà MD ⊥ DE

Nên EN // MD (quan hệ từ vuông góc đến song song)

Xét tứ giác DENM có EN ⊥ DE, EN // MD (chứng minh trên)

Suy ra DENM là hình thang vuông

Do đó \({S_{DENM}} = \frac{{\left( {DM + EN} \right).DE}}{2} = \frac{{\left( {2 + 4,5} \right).6}}{2} = 19,5\,\,\left( {c{m^2}} \right)\) .

Lời giải

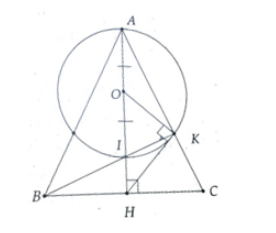
a) Vì BK là đường cao của tam giác ABC nên \(\widehat {AKB} = 90^\circ \)

Suy ra tam giác AKI vuông tại K

Do đó K thuộc đường tròn đường kính AI

b) Gọi O là trung điểm của AI

Vì OA = OK nên tam giác OAK cân tại O

Suy ra \(\widehat {OAK} = \widehat {OK{\rm{A}}}\)

Vì tam giác BCK vuông ở K nên \(\widehat {KBC} + \widehat {KCB} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)

Vì tam giác ACH vuông ở H nên \(\widehat {HAC} + \widehat {HCA} = 90^\circ \) (trong tam giác vuông tổng hai góc nhọn bằng 90°)

Suy ra \(\widehat {KBC} = \widehat {HAC}\)

Mà \(\widehat {OAK} = \widehat {OK{\rm{A}}}\) (chứng minh trên)

Suy ra \(\widehat {KBC} = \widehat {OK{\rm{A}}}\)                           (1)

Vì tam giác ABC cân tại A, AH là đường cao

Nên AH là đường trung tuyến

Hay H là trung điểm của BC

Xét tam giác BCK vuông ở K có KH là trung tuyến

Suy ra BH = HK

Do đó tam giác BHK cân tại H

Suy ra \(\widehat {BHK} = \widehat {BKH}\)                            (2)

Từ (1) và (2) suy ra \(\widehat {AKO} = \widehat {BKH}\)

Mà \(\widehat {AKO} + \widehat {OKB} = \widehat {AKB} = 90^\circ \)

Suy ra \(\widehat {BKO} + \widehat {BKH} = 90^\circ \)

Hay \(\widehat {HOK} = 90^\circ \)

Xét (O) có OH ⊥ HK

Suy ra HK là tiếp tuyến của (O)

Vậy HK là tiếp tuyến của đường tròn đường kính AI.