Câu hỏi:

13/07/2024 1,022

Cho khối lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a. Tính thể tích khối tứ diện A’BB’C’?

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải

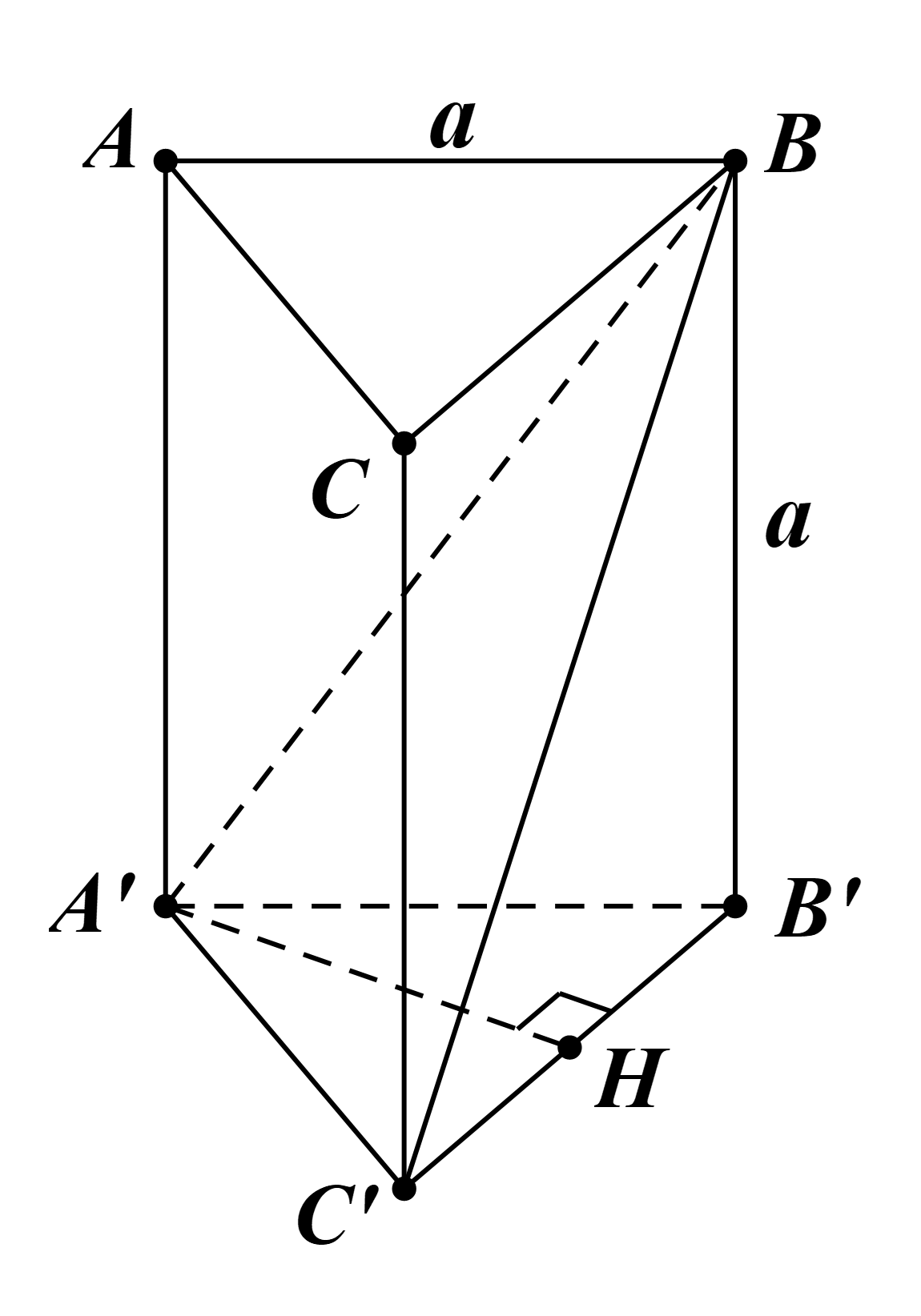
Media VietJack

Do ABC.A’B’C’ là khối lăng trụ đứng nên BB’ ⊥ (A’B’C’).

Kẻ A’H’ ⊥ B’C’.

Khối lăng trụ đứng tam giác ABC.A’B’C’ có tất cả các cạnh đều bằng a.

Suy ra BB’ = A’B’ = B’C’ = a.

Do ∆A’B’C’ đều nên A’H vừa là đường cao, vừa là đường trung tuyến của ∆A’B’C’.

Suy ra \[B'H = \frac{{B'C'}}{2} = \frac{a}{2}\].

∆A’B’H vuông tại H: \(A'H = \sqrt {A'{{B'}^2} - B'H} = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\).

Thể tích khối tứ diện A’BB’C’ là:

\(V = \frac{1}{3}BB'.{S_{A'B'C'}} = \frac{1}{3}a.\frac{1}{2}A'H.B'C' = \frac{1}{6}.a.\frac{{a\sqrt 3 }}{2}.a = \frac{{{a^3}\sqrt 3 }}{{12}}\).

Vậy thể tích khối tứ diện A’BB’C’ bằng \(\frac{{{a^3}\sqrt 3 }}{{12}}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì (M khác A), kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.

1) Chứng minh tứ giác AMBO nội tiếp.

2) Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn.

3) Chứng minh OI.OM = R²; OI.IM = IA².

4) Chứng minh OAHB là hình thoi.

5) Chứng minh ba điểm O, H, M thẳng hàng.

6) Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d.

Xem đáp án

Lời giải

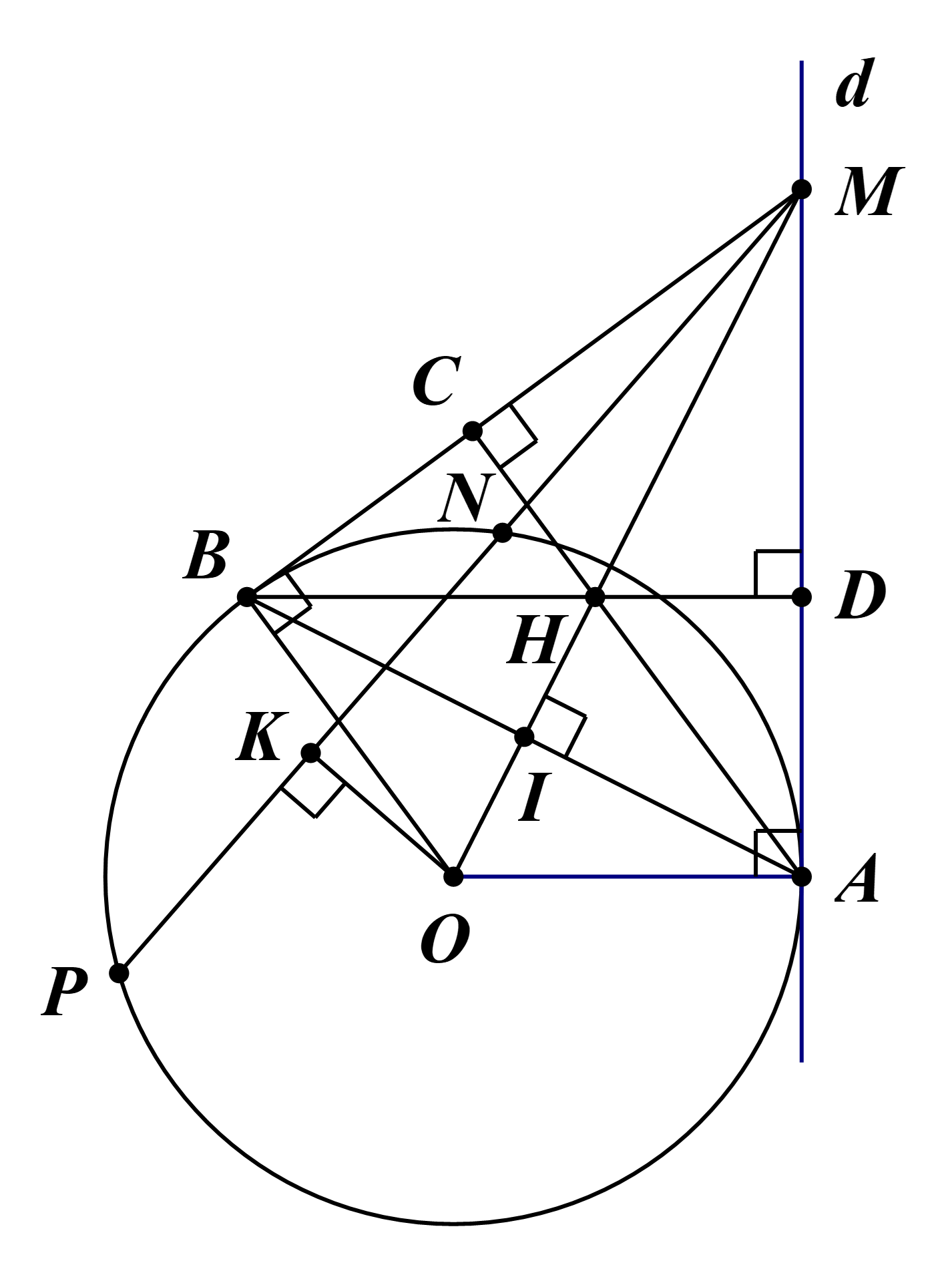
Media VietJack

1) Ta có \(\widehat {OAM} = 90^\circ \) (do MA là tiếp tuyến của (O), A là tiếp điểm).

Suy ra ba điểm O, A, M cùng thuộc một đường tròn đường kính OM (1)

Lại có \(\widehat {OBM} = 90^\circ \) (do MB là tiếp tuyến của (O), B là tiếp điểm).

Suy ra ba điểm O, B, M cùng thuộc một đường tròn đường kính OM (2)

Từ (1), (2), ta được tứ giác AMBO nội tiếp đường tròn đường kính OM.

2) Đường tròn (O) có NP là dây cung.

Mà K là trung điểm của NP (giả thiết).

Suy ra OK ⊥ NP tại K hay \(\widehat {OKM} = 90^\circ \).

Do đó ba điểm O, K, M cùng thuộc một đường tròn đường kính OM.

Mà từ kết quả câu 1), ta có bốn điểm A, M, B, O cùng thuộc một đường tròn đường kính OM.

Vậy năm điểm O, K, A, M, B cùng nằm trên một đường tròn đường kính OM.

3) Từ kết quả câu 1), ta có tứ giác AMBO nội tiếp đường tròn đường kính OM.

Suy ra AB là dây cung của đường tròn đường kính OM.

Do đó OM ⊥ AB.

∆OAM vuông tại A có AI là đường cao.

Áp dụng hệ thức lượng trong tam giác vuông, ta có: OA² = OI.OM và OI.IM = IA².

⇔ OI.OM = R² và OI.IM = IA².

Vậy ta có điều phải chứng minh.

4) Ta có OA ⊥ AM (do AM là tiếp tuyến của (O) và BD ⊥ MA (giả thiết).

Suy ra OA // BD.

Chứng minh tương tự, ta được OB // AC.

Do đó tứ giác OAHB là hình bình hành.

Mà OA = OB = R.

Vậy tứ giác OAHB là hình thoi.

5) Ta có OH ⊥ AB (do tứ giác OAHB là hình thoi).

Mà OM ⊥ AB (theo kết quả câu 3).

Do đó OM ≡ OH.

Vậy ba điểm O, H, M thẳng hàng.

6) Do d là tiếp tuyến của đường tròn (O) nên mọi điểm đều nằm cùng một phía đối với d.

Ta có OAHB là hình thoi (kết quả câu 4).

Suy ra AH = OA = R.

Do đó khi M di động trên d thì H cũng di động nhưng luôn cách A một khoảng cố định bằng R.

Vậy quỹ tích của điểm H khi M di chuyển trên đường thẳng d là nửa đường tròn tâm A, bán kính AH = R.

Câu 2

Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của CC’. Khoảng cách từ M đến mặt phẳng (A’BC) bằng

A. \(\frac{{\sqrt {21} a}}{7}\);

B. \(\frac{{\sqrt {21} a}}{{14}}\);

C. \(\frac{{\sqrt 2 a}}{4}\);

D. \(\frac{{\sqrt 2 a}}{2}\).

Lời giải

Đáp án đúng là: B

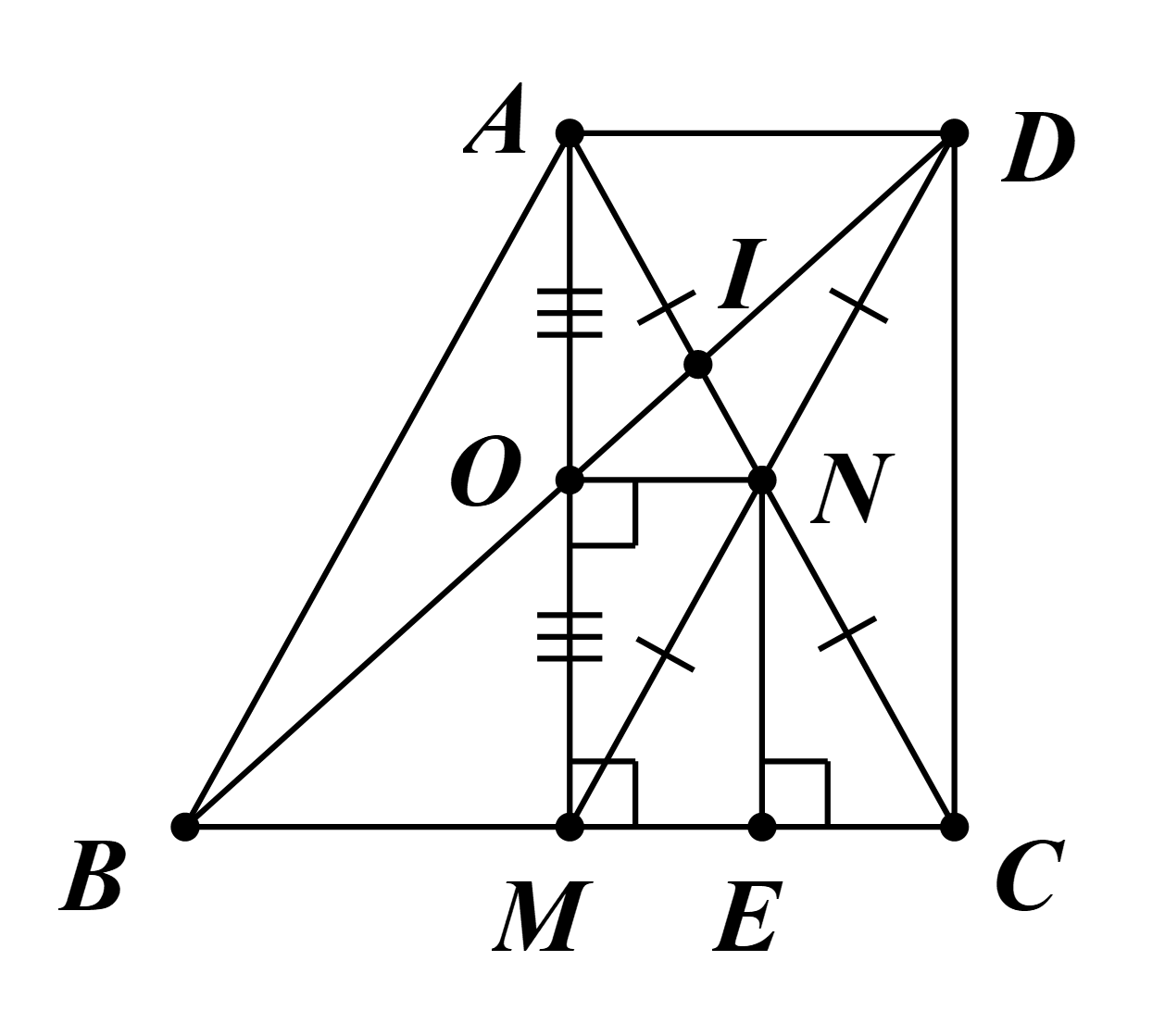
Media VietJack

Ta có C = C’M ∩ (A’BC).

Suy ra \(\frac{{d\left( {M,\,\left( {A'BC} \right)} \right)}}{{d\left( {C',\,\left( {A'BC} \right)} \right)}} = \frac{{CM}}{{CC'}} = \frac{1}{2}\) (do M là trung điểm CC’).

Hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh bằng a.

Suy ra AA’ ⊥ (ABC) và AA’ = AB = BC = a.

Ta có \({V_{C'.ABC}} = \frac{1}{3}{V_{ABC.A'B'C'}} = \frac{1}{3}.CC'.{S_{\Delta ABC}} = \frac{1}{3}.a.\frac{1}{2}.AB.AC.\sin \widehat {BAC}\)

\( = \frac{1}{6}.a.a.a.\sin 60^\circ = \frac{{{a^3}\sqrt 3 }}{{12}}\).

∆AA’B vuông tại A: \(A'B = \sqrt {A{{A'}^2} + A{B^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \).

Chứng minh tương tự, ta được \(A'C = a\sqrt 2 \).

Nửa chu vi ∆A’BC là: \(p = \frac{{A'C + A'B + BC}}{2} = \frac{{a\sqrt 2 + a\sqrt 2 + a}}{2} = \frac{{\left( {2\sqrt 2 + 1} \right)a}}{2}\).

Ta có \({S_{\Delta A'BC}} = \sqrt {p\left( {p - A'C} \right)\left( {p - A'B} \right)\left( {p - BC} \right)} \)

\( = \sqrt {\frac{{\left( {2\sqrt 2 + 1} \right)a}}{2}\left( {\frac{{\left( {2\sqrt 2 + 1} \right)a}}{2} - a\sqrt 2 } \right)\left( {\frac{{\left( {2\sqrt 2 + 1} \right)a}}{2} - a\sqrt 2 } \right)\left( {\frac{{\left( {2\sqrt 2 + 1} \right)a}}{2} - a} \right)} = \frac{{{a^2}\sqrt 7 }}{4}\).

Ta có \(d\left( {C',\left( {A'BC} \right)} \right) = \frac{{3{V_{C'.A'BC}}}}{{{S_{\Delta A'BC}}}} = \frac{{3.\frac{{{a^3}\sqrt 3 }}{{12}}}}{{\frac{{{a^2}\sqrt 7 }}{4}}} = \frac{{a\sqrt {21} }}{7}\).

Vì vậy \(d\left( {M,\,\left( {A'BC} \right)} \right) = \frac{1}{2}d\left( {C',\,\left( {A'BC} \right)} \right) = \frac{1}{2}.\frac{{a\sqrt {21} }}{7} = \frac{{a\sqrt {21} }}{{14}}\).

Vậy ta chọn phương án B.

Câu 3