Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy C1, A1, B1 sao cho các đường thẳng AA1, BB1, CC1 đồng quy tại O. Đường thẳng qua O // AC cắt A1B1, B1C1, tại K và M tương ứng. Chứng minh rằng: OK = OM.
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy C1, A1, B1 sao cho các đường thẳng AA1, BB1, CC1 đồng quy tại O. Đường thẳng qua O // AC cắt A1B1, B1C1, tại K và M tương ứng. Chứng minh rằng: OK = OM.
Quảng cáo
Trả lời:
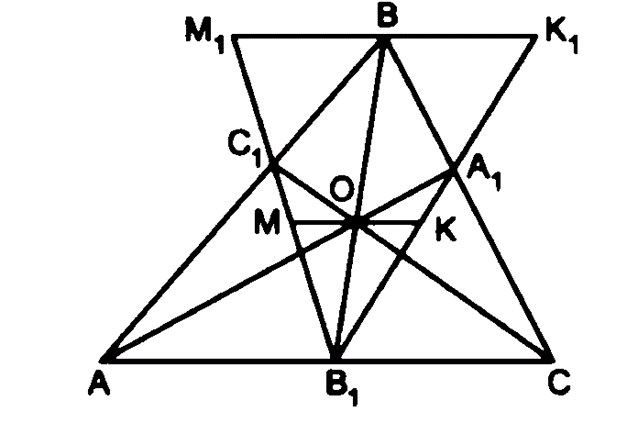
Qua B vẽ đường thẳng song song với AC cắt A1B1 và B1C1 lần lượt tại K1 và M1.
Theo giả thiết: MK // AC
Mà M1K1 // AC (theo cách vẽ)
Suy ra: MK // M1K1.
Xét tam giác B1K1M1 có MK // M1K1 suy ra: \(\frac{{MO}}{{B{M_1}}}\, = \,\,\frac{{OK}}{{B{K_1}}}\,\)(*)
Xét tam giác AB1C1 và tam giác BM1C1 có:
\(\widehat {A{C_1}{B_1}} = \,\widehat {B{C_1}{M_1}}\)(2 góc đối đỉnh)
\(\widehat {A{B_1}{C_1}} = \,\widehat {B{M_1}{C_1}}\)(2 góc so le trong vì AC // M1K1)
Suy ra: ∆ AB1C1 ᔕ ∆ BM1C1 (g.g)
Nên \(\frac{{B{M_1}}}{{A{B_1}}}\, = \,\frac{{B{C_1}}}{{A{C_1}}}\)⇒ \(B{M_1} = A{B_1}\,.\,\,\frac{{B{C_1}}}{{A{C_1}}}\)(1)
Tương tự: ∆ CB1A1 ᔕ ∆ BK1A1 (g.g)
Nên \(\frac{{B{K_1}}}{{C{B_1}}}\, = \,\frac{{B{A_1}}}{{C{A_1}}}\)⇒ \(B{K_1} = C{B_1}\,.\,\,\frac{{B{A_1}}}{{C{A_1}}}\)(2)
Lấy (1) chia (2) ta được: \(\frac{{B{M_1}}}{{B{K_1}}}\, = \frac{{A{B_1}}}{{B{C_1}}}\,.\,\,\frac{{C{A_1}}}{{B{A_1}}}\,.\,\frac{{C{B_1}}}{{A{C_1}}}\,\, = \,\,1\) (áp dụng định lí Xê–va)
Suy ra: BM1 = BK1 (**)
Từ (*) và (**), ta có: OM = OK
Vậy OM = OK.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi thêm 4 đơn vị vào số bị chia, phép chia khi đó sẽ dư:
4 + 1 = 5
Thì khi ấy phép chia là phép chia hết
Vậy cần tăng thêm 4 đơn vị vào số bị chia.
Lời giải
Ban đầu Hùng có nhiều hơn Dũng:
14 – 5 = 9 (viên bi).
Theo đề bài ta có sơ đồ:
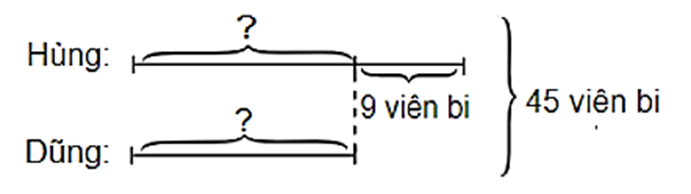
Số viên bi của bạn Hùng là:
(45 + 9) : 2 = 27 (viên bi).
Số viên bi của bạn Dũng là:
27 – 9 = 18 (viên bi).
Đáp số: Hùng: 27 viên bi; Dũng: 18 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.