Chứng minh rằng \(\left| a \right| + \left| b \right|\, \ge \,\left| {a + b} \right|\) với mọi a, b ∈ ℝ.
Chứng minh rằng \(\left| a \right| + \left| b \right|\, \ge \,\left| {a + b} \right|\) với mọi a, b ∈ ℝ.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Ta có: \(\left| a \right|,\left| b \right|\,,\,\left| {a + b} \right|\,\, \ge \,0\)
Suy ra bất đẳng thức tương đương: \(\left( {\left| a \right| + \left| b \right|} \right){\,^2}\, \ge \,\,{\left( {\left| {a + b} \right|} \right)^2}\)
⇔ \(\left| {ab} \right| \ge \,\,ab\)(đúng)
Dấu “=” xảy ra khi ab ≥ 0.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi thêm 4 đơn vị vào số bị chia, phép chia khi đó sẽ dư:
4 + 1 = 5
Thì khi ấy phép chia là phép chia hết
Vậy cần tăng thêm 4 đơn vị vào số bị chia.
Lời giải
Ban đầu Hùng có nhiều hơn Dũng:
14 – 5 = 9 (viên bi).
Theo đề bài ta có sơ đồ:
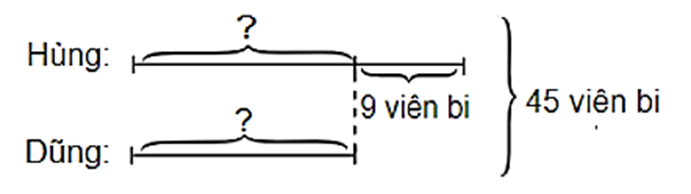
Số viên bi của bạn Hùng là:
(45 + 9) : 2 = 27 (viên bi).
Số viên bi của bạn Dũng là:
27 – 9 = 18 (viên bi).
Đáp số: Hùng: 27 viên bi; Dũng: 18 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.