Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh BE2 + CF2 ≥ EF2, khi nào dấu “=” xảy ra?
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F. Chứng minh BE2 + CF2 ≥ EF2, khi nào dấu “=” xảy ra?
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
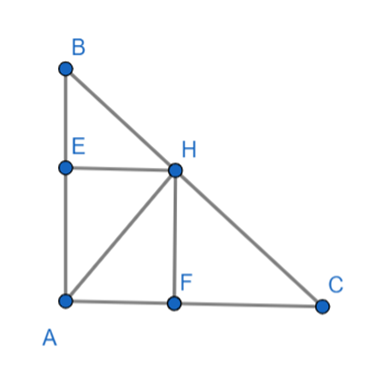
Xét tam giác CFH và tam giác CAB có:
\(\widehat C\) chung
\(\widehat {CFH} = \widehat {CAB}\)(bằng 90 độ)
Suy ra: ∆CFH ᔕ ∆CAB (g.g)
Nên: \[\frac{{CF}}{{CA}} = \frac{{CH}}{{CB}}\,\,hay\,\,\frac{{CF}}{{CH}} = \frac{{CA}}{{CB}}\, \Rightarrow \,C{F^2} = \frac{{C{A^2}\,.\,C{H^2}\,}}{{C{B^2}}} = \frac{{C{H^3}\,}}{{CB}}\]( vì CA = CH.CB) (1)
Tương tự: ∆BEH ᔕ ∆BAC (g.g)
Suy ra: \[\frac{{BE}}{{BH}} = \frac{{BA}}{{BC}}\,\, \Rightarrow \,B{E^2} = \frac{{B{A^2}\,.\,B{H^2}\,}}{{B{C^2}}} = \frac{{B{H^3}}}{{BC}}\](vì BA2 = BH. BC) (2)
TỪ (1) và (2) ta có:
\[\sqrt[3]{{B{E^2}}} + {\rm{ }}\sqrt[3]{{C{F^2}}} = \,\frac{{BH + CH}}{{\sqrt[3]{{BC}}}} = \sqrt[3]{{B{C^2}}}\]
Áp dụng bất đẳng thức: a3 + b3 ≥ \[\frac{{{{\left( {a + b} \right)}^3}}}{4}\] ta có:
BE2 + CF2 ≥ \[\frac{{{{\left( {\sqrt[3]{{B{E^2}}} + \sqrt[3]{{C{F^2}}}} \right)}^2}}}{4} = \frac{{B{C^2}}}{4}\]
MÀ AH ≤ \(\frac{1}{2}BC\)(vì AH luôn nhỏ hơn đường trung tuyến kẻ từ A xuống BC)
Suy ra: AH2 ≤ \(\frac{1}{4}B{C^2}\)
Mặt khác: AHEF là hình chữ nhật (vì có 3 góc vuông) nên AH = EF
Vậy: BE2 + CF2 ≥ EF2
Dấu “=” khi tam giác ABC vuông cân tại A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi thêm 4 đơn vị vào số bị chia, phép chia khi đó sẽ dư:
4 + 1 = 5
Thì khi ấy phép chia là phép chia hết
Vậy cần tăng thêm 4 đơn vị vào số bị chia.
Lời giải
Ban đầu Hùng có nhiều hơn Dũng:
14 – 5 = 9 (viên bi).
Theo đề bài ta có sơ đồ:
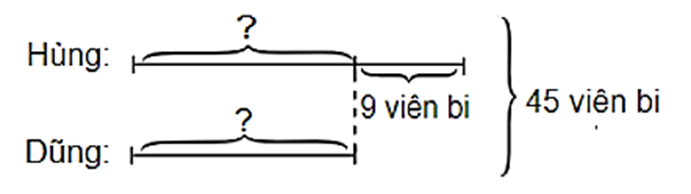
Số viên bi của bạn Hùng là:
(45 + 9) : 2 = 27 (viên bi).
Số viên bi của bạn Dũng là:
27 – 9 = 18 (viên bi).
Đáp số: Hùng: 27 viên bi; Dũng: 18 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.