Giả sử ABC là tam giác nhọn nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:
a, BC song song với DE.
b, Tứ giác BCED là hình thang cân.
Giả sử ABC là tam giác nhọn nội tiếp đường tròn (O). Đường cao AH cắt đường tròn (O) tại D. Kẻ đường kính AE của đường tròn (O). Chứng minh:
a, BC song song với DE.
b, Tứ giác BCED là hình thang cân.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
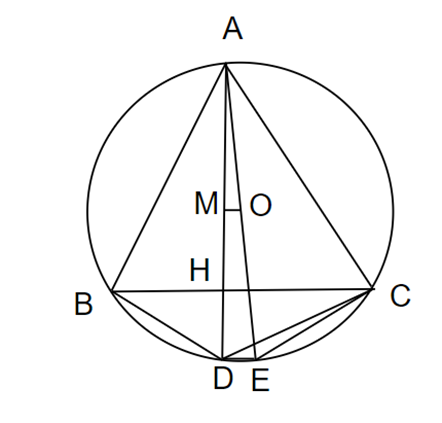
a) Từ O kẻ OM vuông góc với AD
Khi đó theo tính chất của đường kính và dây cung thì M là trung điểm AD
Lại có O là trung điểm AE ⇒ MO là đường trung bình của tam giác ADE
⇒ MO // DE , lại có MO // BC (cùng vuông góc với AD)
⇒ DE // BC.
b) Tứ giác ABDC nội tiếp đường tròn (O) suy ra \[\widehat {ADB} = \widehat {BCA}\]
hay 90° – \(\widehat {ADB}\)= 90° – \(\widehat {BCA}\)
Suy ra: \(\widehat {CBD} = \widehat {ECB}\)
Theo phần a, vì BC // DE nên BCDE là hình thang
Vậy: BCDE là hình thang cân.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khi thêm 4 đơn vị vào số bị chia, phép chia khi đó sẽ dư:
4 + 1 = 5
Thì khi ấy phép chia là phép chia hết
Vậy cần tăng thêm 4 đơn vị vào số bị chia.
Lời giải
Ban đầu Hùng có nhiều hơn Dũng:
14 – 5 = 9 (viên bi).
Theo đề bài ta có sơ đồ:
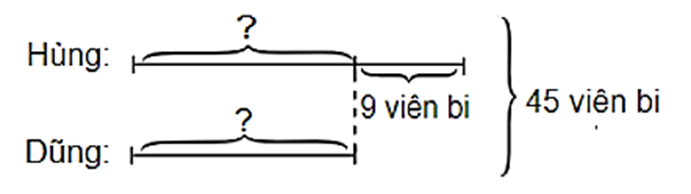
Số viên bi của bạn Hùng là:
(45 + 9) : 2 = 27 (viên bi).
Số viên bi của bạn Dũng là:
27 – 9 = 18 (viên bi).
Đáp số: Hùng: 27 viên bi; Dũng: 18 viên bi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.