Cho H, K là các giao điểm của đường tròn (O1), (O2). Đường thẳng O1H cắt (O1) tại A, (O2) tại B. O2H cắt (O1) tại C và (O2) tại D. Chứng minh rằng ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.

Gọi E là giao điểm của AC và BD. Vì các tam giác ACH, AKH nội tiếp đường tròn (O1) có cạnh HA là đường kính nên tam giác ACH vuông tại C và tam giác AKH vuông tại K. Suy ra DC⊥AEHK⊥AK 12 Vì các tam giác HDK, HDB nội tiếp đường tròn (O2) có cạnh HD là đường kính nên tam giác HDK vuông tại K và tam giác HBD vuông tại B. Suy ra AB⊥DEHK⊥KD 34 Từ (2), (4), suy ra ba điểm A, K, D thẳng hàng. Do đó HK ⊥ AD. Từ (1), (3), suy ra H là trực tâm của tam giác AED. Do đó HE ⊥ AD. Vì vậy H ∈ EK. Vậy ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.

Câu hỏi:

19/08/2025 665

Cho H, K là các giao điểm của đường tròn (O₁), (O₂). Đường thẳng O₁H cắt (O₁) tại A, (O₂) tại B. O₂H cắt (O₁) tại C và (O₂) tại D. Chứng minh rằng ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

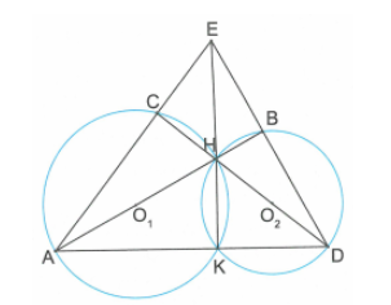
Cho H, K là các giao điểm của đường tròn (O1), (O2). Đường thẳng O1H cắt (O1) tại A, (O2) tại B. O2H cắt (O1) tại C và (O2) tại D. Chứng minh rằng ba đường thẳng AC, BD, HK đồng quy tại 1 điểm. (ảnh 1)

Gọi E là giao điểm của AC và BD.

Vì các tam giác ACH, AKH nội tiếp đường tròn (O₁) có cạnh HA là đường kính nên tam giác ACH vuông tại C và tam giác AKH vuông tại K.

Suy ra $\{\begin{cases} D C ⊥ A E \\ H K ⊥ A K \end{cases} \begin{matrix} (1) \\ (2) \end{matrix}$

Vì các tam giác HDK, HDB nội tiếp đường tròn (O₂) có cạnh HD là đường kính nên tam giác HDK vuông tại K và tam giác HBD vuông tại B.

Suy ra $\{\begin{cases} A B ⊥ D E \\ H K ⊥ K D \end{cases} \begin{matrix} (3) \\ (4) \end{matrix}$

Từ (2), (4), suy ra ba điểm A, K, D thẳng hàng.

Do đó HK ⊥ AD.

Từ (1), (3), suy ra H là trực tâm của tam giác AED.

Do đó HE ⊥ AD.

Vì vậy H ∈ EK.

Vậy ba đường thẳng AC, BD, HK đồng quy tại 1 điểm.

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tính nhanh: 1.2 + 2.3 + 3.4 + ... + 98.99.

Xem đáp án

Lời giải

Đặt A = 1.2 + 2.3 + 3.4 + ... + 98.99.

Suy ra 3A = 1.2.3 + 2.3.3 + 3.4.3 + ... + 98.99.3.

= 1.2.3 + 2.3.(4 – 1) + 3.4.(5 – 2) + ... + 98.99.(100 – 97).

= 1.2.3 + 2.3.4 – 1.2.3 + 3.4.5 – 2.3.4 + ... + 98.99.100 – 97.98.99.

= 98.99.100

Suy ra A = 98.99.100 : 3 = 98.33.100 = 323 400.

Vậy A = 323 400.

Câu 2

Số học sinh của một trường là một số tự nhiên có 3 chữ số và lớn hơn 900. Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng. Tính số học sinh của trường đó?

Xem đáp án

Lời giải

Gọi số học sinh của trường đó là x (900 < x < 1000 và x ∈ ℕ).

Mỗi lần xếp hàng 3, hàng 4, hàng 5 đều không có ai lẻ hàng.

Suy ra x chia hết cho 3, 4, 5 hay x là BC(3, 4, 5).

Mà BCNN(3, 4, 5) = 60.

Do đó x ∈ B(60) = {0; 60; 120; 180; 240; 300; ...}.

Mà 900 < x < 1000 và x ∈ ℕ nên x = 960.

Vậy số học sinh của trường đó là 960.

Câu 3