Cho hình vuông ABCD. Qua A vẽ 2 đường thẳng vuông góc với nhau, cắt BC tại Q và R, cắt CD tại P và S.
a) Tam giác AQR và APS là tam giác cân.
Cho hình vuông ABCD. Qua A vẽ 2 đường thẳng vuông góc với nhau, cắt BC tại Q và R, cắt CD tại P và S.
a) Tam giác AQR và APS là tam giác cân.
Quảng cáo
Trả lời:
Giải bởi Vietjack
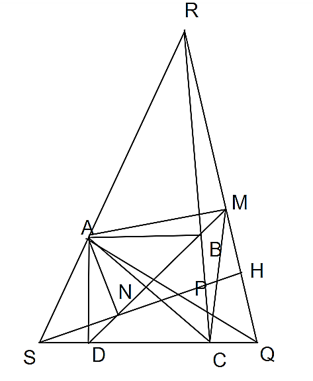
a) Xét tam giác vuông ABR và ADQ có:
AB = AD (giả thiết)
= 90°
Góc = 90°
⇒
⇒ ∆ABR = ∆ADQ (cạnh góc vuông – góc nhọn kề)
⇒ AR = AQ (2 cạnh tương ứng)
⇒ Tam giác AQR cân tại A.
Chứng minh tương tự: ta có ∆ADS = ∆ABP
⇒ AS = AP ⇒ ∆APS cân tại A.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích căn phòng đó là:
12 . 8 = 96 (m²)
Diện tích một viên gạch là:
40 . 40 =1600 (cm²)
Đổi: 1600 cm² = 0,16m²
Số gạch dùng để lát nền là:
96 : 0,16 = 600 (viên).
Đáp số: 600 viên gạch.
Lời giải
Theo bài ra ta có:
4n + 9 ⋮ 2n + 1
⇔ 4n + 2 + 7 ⋮ 2n + 1
⇔ 2(2n + 1) +7 ⋮ 2n + 1
⇒ 7 ⋮ 2n + 1
Suy ra: 2n + 1 ∈ Ư(7) = {1; 7}
Vậy n ∈ {0; 3}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo