Cho hàm số \[\frac{1}{4}{x^2}\] có đồ thị (P) và I(0; 3).
a) Tìm tọa độ giao điểm A và B của (P) và đường thẳng y = 2x – 3.
b) Tính độ dài AB.
c) Tính diện tích tam giác OAB.
d) Tìm tọa độ điểm M trên (P) sao cho độ dài MI nhỏ nhất.
Cho hàm số \[\frac{1}{4}{x^2}\] có đồ thị (P) và I(0; 3).
a) Tìm tọa độ giao điểm A và B của (P) và đường thẳng y = 2x – 3.
b) Tính độ dài AB.
c) Tính diện tích tam giác OAB.
d) Tìm tọa độ điểm M trên (P) sao cho độ dài MI nhỏ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Phương trình hoành độ giao điểm của (P) và y = 2x – 3 là: \[\frac{1}{4}{x^2} = 2x - 3\].
⇔ x2 – 8x + 12 = 0.
⇔ x = 6 hoặc x = 2.
Với x = 6, ta có: y = 2.6 – 3 = 9.
Suy ra tọa độ A(6; 9).
Với x = 2, ta có: y = 2.2 – 3 = 1.
Suy ra tọa độ B(2; 1).
Vậy A(6; 9) và B(2; 1).
b)
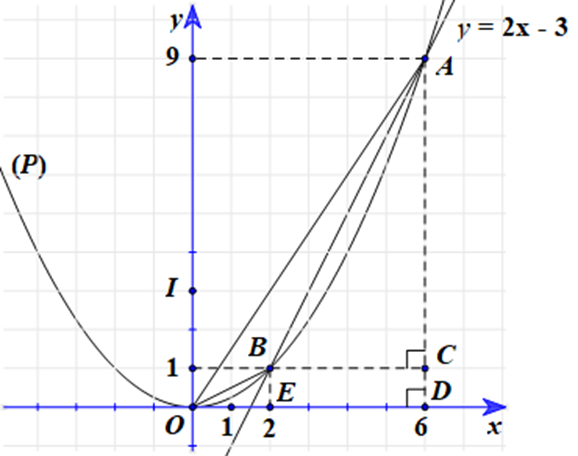
Ta có BC = 6 – 2 = 4, AC = 9 – 1 = 8.
Tam giác ABC vuông tại C: AB2 = AC2 + BC2 = 82 + 42 = 80.
Suy ra \(AB = 4\sqrt 5 \).
c) Ta có OE = 2, BE = 1, AD = 9, OD = 6, DE = BC = 4.
Lại có:
⦁ \({S_{\Delta OAD}} = \frac{1}{2}OD.AD = \frac{1}{2}.6.9 = 27\);
⦁ \({S_{\Delta OBE}} = \frac{1}{2}OE.BE = \frac{1}{2}.2.1 = 1\);
⦁ \({S_{BEDA}} = \frac{{DE.\left( {BE + AD} \right)}}{2} = \frac{{4.\left( {1 + 9} \right)}}{2} = 20\).
Khi đó ta có SOAB = SOAD – SOBE – SBEDA = 27 – 1 – 20 = 6.
Vậy SOAB = 6 (đvS).
d) Do M ∈ (P) nên tọa độ M có dạng \(M\left( {m;\frac{{{m^2}}}{4}} \right)\).
Suy ra \(IM = \sqrt {{m^2} + {{\left( {\frac{{{m^2}}}{4} - 3} \right)}^2}} = \sqrt {{{\left( {\frac{{{m^2}}}{4} - \frac{1}{2}} \right)}^2} + \frac{{35}}{4}} \ge \frac{{\sqrt {35} }}{2}\).
Dấu “=” xảy ra \( \Leftrightarrow \frac{{{m^2}}}{4} = \frac{1}{2} \Leftrightarrow m = \pm \sqrt 2 \).
Với \(m = \sqrt 2 \), ta có tọa độ \(M\left( {\sqrt 2 ;\frac{1}{2}} \right)\).
Với \(m = - \sqrt 2 \), ta có tọa độ \(M\left( { - \sqrt 2 ;\frac{1}{2}} \right)\).
Vậy \(M\left( {\sqrt 2 ;\frac{1}{2}} \right)\) và \(M\left( { - \sqrt 2 ;\frac{1}{2}} \right)\) thỏa mãn yêu cầu bài toán.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
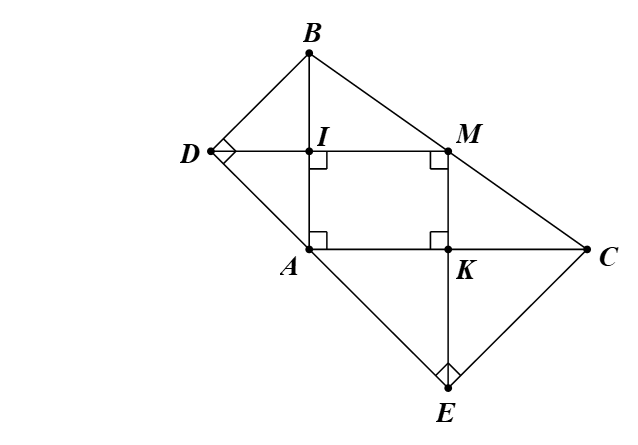
a) Ta có tam giác ADB vuông cân tại D.
Suy ra \(\widehat {DAB} = 45^\circ \).
Chứng minh tương tự, ta được \(\widehat {CAE} = 45^\circ \).
Ta có \(\widehat {DAB} + \widehat {BAC} + \widehat {CAE} = 45^\circ + 90^\circ + 45^\circ = 180^\circ \).
Vậy ba điểm D, A, E thẳng hàng.
b) Tam giác ABC vuông tại A có AM là đường trung tuyến.
Suy ra MA = MB = MC.
Do đó M nằm trên đường trung trực của đoạn AB (1)
Chứng minh tương tự, ta được D nằm trên đường trung trực của đoạn AB (2)
Từ (1), (2), suy ra DM là đường trung trực của đoạn AB.
Mà DM cắt AB tại I.
Do đó DM ⊥ AB tại I.
Chứng minh tương tự, ta được ME ⊥ AC tại K.
Tứ giác IAKM, có: \(\widehat {MIA} = \widehat {IAK} = \widehat {AKM} = 90^\circ \).
Vậy tứ giác IAKM là hình chữ nhật.
c) Tam giác ADB vuông cân tại D có DI là đường cao.
Suy ra DI cũng là đường phân giác của tam giác ADB.
Do đó \[\widehat {ADI} = 90^\circ :2 = 45^\circ \].
Mà \(\widehat {DME} = 90^\circ \) (do tứ giác IAKM là hình chữ nhật).
Vậy tam giác DME là tam giác vuông cân tại M.
Lời giải
Ta có 3(x2 + x)2 – 2x2 – 2x = 0.
⇔ 3(x2 + x)2 – 2(x2 + x) = 0.
⇔ (x2 + x)[3(x2 + x) – 2] = 0.
\[ \Leftrightarrow \left[ \begin{array}{l}{x^2} + x = 0\\3{x^2} + 3x - 2 = 0\end{array} \right.\]
\[ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = \frac{{ - 3 \pm \sqrt {33} }}{6}\end{array} \right.\]
Vì vậy \(A = \left\{ {0; - 1;\frac{{ - 3 \pm \sqrt {33} }}{6}} \right\}\).
Vậy số tập con của tập A là 23 = 8 tập con.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo