Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của AC và BD. Gọi M, N lần lượt là trung điểm của SB, SC. Tính tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
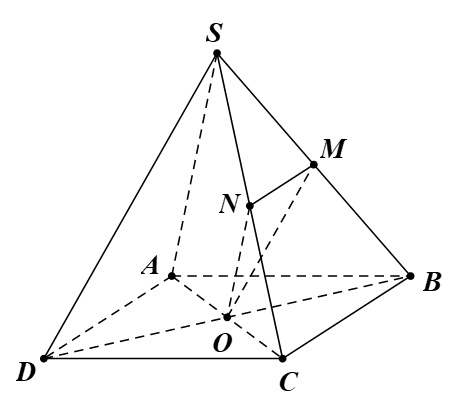
Ta có \(\frac{{d\left( {O,\left( {BCNM} \right)} \right)}}{{d\left( {A,\left( {BCNM} \right)} \right)}} = \frac{{CO}}{{CA}} = \frac{1}{2}\) (do O là trung điểm AC).
\( \Rightarrow d\left( {O,\left( {BCNM} \right)} \right) = \frac{1}{2}d\left( {A,\left( {BCNM} \right)} \right)\).
Lại có \({S_{SMN}} = \frac{1}{2}SM.SN.\sin \widehat {MSN} = \frac{1}{8}SB.SC.\sin \widehat {MSN} = \frac{1}{4}{S_{SBC}}\).
Suy ra \({S_{BCNM}} = {S_{SBC}} - {S_{SMN}} = {S_{SBC}} - \frac{1}{4}{S_{SBC}} = \frac{3}{4}{S_{SBC}}\).
Ta có \({S_{ABC}} = \frac{1}{2}d\left( {A,CD} \right).CD\) và SABCD = d(A, CD).CD.
Suy ra \({S_{ABC}} = \frac{1}{2}{S_{ABCD}}\).
Vì vậy \({V_{O.BCNM}} = \frac{1}{3}d\left( {O,\left( {BCNM} \right)} \right).{S_{BCNM}} = \frac{1}{3}.\frac{1}{2}d\left( {A,\left( {BCNM} \right)} \right).\frac{3}{4}{S_{SBC}}\).
\( = \frac{3}{8}{V_{SABC}} = \frac{3}{8}.\frac{1}{3}d\left( {S,\left( {ABC} \right)} \right).{S_{ABC}} = \frac{3}{8}.\frac{1}{3}d\left( {S,\left( {ABCD} \right)} \right).\frac{1}{2}{S_{ABCD}} = \frac{3}{{16}}{V_{S.ABCD}}\).
Suy ra \(\frac{{{V_{O.BCNM}}}}{{{V_{S.ABCD}}}} = \frac{3}{{16}}\).
Vậy tỉ số thể tích giữa hai khối chóp O.BCNM và S.ABCD là \(\frac{3}{{16}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

a) Hình bình hành ABCD có \(\widehat {BAD},\,\widehat {ADC}\) ở vị trí trong cùng phía.
Suy ra \(\widehat {ADC} = 180^\circ - \widehat {BAD} = 60^\circ \).
Khi đó \(\widehat {ADI} = \widehat {IDC} = \frac{{\widehat {ADC}}}{2} = 30^\circ \) (do DI là tia phân giác của \(\widehat {ADC}\)).
Mà \(\widehat {AID} = \widehat {IDC}\) (cặp góc so le trong).
Vì vậy \(\widehat {AID} = \widehat {ADI}\).
Suy ra tam giác ADI cân tại A.
Do đó AD = AI.
Mà AB = 2AI (I là trung điểm của AB).
Vậy AB = 2AD (điều phải chứng minh).
b) Gọi J là trung điểm của DI.
Tam giác ADI có AJ là đường trung tuyến.
Suy ra AJ vừa là đường phân giác, vừa là đường cao của tam giác ADI.
Khi đó \(\widehat {JAI} = \widehat {DAJ} = \frac{{\widehat {DAI}}}{2} = 60^\circ \).
Xét ∆AJD và ∆DHA, có:
\(\widehat {AJD} = \widehat {DHA} = 90^\circ \);
AD là cạnh chung;
\(\widehat {DAJ} = \widehat {ADH} = 60^\circ \).
Do đó ∆AJD = ∆DHA (cạnh huyền – góc nhọn).
Suy ra DJ = AH (cặp cạnh tương ứng).
Mà DI = 2DJ (J là trung điểm của DI).
Vậy DI = 2AH (điều phải chứng minh).
c) Ta có BI = BC \(\left( { = \frac{1}{2}AB} \right)\).
Suy ra tam giác IBC cân tại B.
Mà \(\widehat {IBC} = \widehat {ADC} = 60^\circ \).
Do đó tam giác IBC đều.
Vì vậy IC = IB = IA.
Khi đó tam giác ABC vuông tại C hay \(\widehat {ACB} = 90^\circ \).
Suy ra \(\widehat {DAC} = \widehat {ACB} = 90^\circ \).
Vậy AD ⊥ AC (điều phải chứng minh).
Lời giải
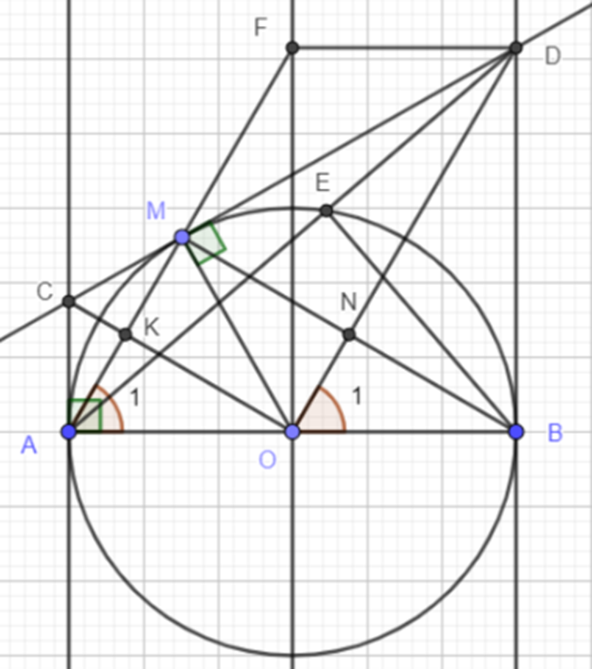
a) Ta có AC là tiếp tuyến của (O). Suy ra AC ⊥ AB (1)
Chứng minh tương tự, ta được BD ⊥ AB (2)
Từ (1), (2), suy ra AC // BD và \[\widehat {BAC} = 90^\circ \].
Vậy ABDC là hình thang vuông.
b) Ta có MD, MB là hai tiếp tuyến của (O).
Suy ra MD = MB.
Do đó D thuộc đường trung trực của đoạn MB (3)
Lại có OB = OM = R.
Suy ra O thuộc đường trung trực của đoạn MB (4)
Từ (3), (4), suy ra OD là đường trung trực của đoạn MB.
Vậy OD ⊥ MB tại N.
Ta có \(\widehat {AEB} = 90^\circ \) và \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn (O)).
Tam giác ABD vuông tại B có BE là đường cao: BD2 = DE.DA (5)
Tam giác BDO vuông tại B có BN là đường cao: BD2 = DN.DO (6)
Từ (5), (6), ta thu được DE.DA = DN.DO.
c) Xét ∆AOF và ∆OBD, có:
\(\widehat {AOF} = \widehat {OBD} = 90^\circ \);
AO = OB (= R);
\(\widehat {{A_1}} = \widehat {{O_1}}\) (cùng phụ với \(\widehat {ABM}\)).
Do đó ∆AOF = ∆OBD (cạnh huyền – góc nhọn).
Suy ra OF = BD (cặp cạnh tương ứng).
Mà OF // BD (cùng vuông góc với AB).
Do đó OFDB là hình bình hành.
Mà \[\widehat {OBD} = 90^\circ \].
Vậy OFDB là hình chữ nhật.
d) Ta có AM = OM = OA = R.
Suy ra tam giác OAM đều.
Do đó \(\widehat {DBM} = \widehat {{A_1}} = 60^\circ \) (cùng phụ với \(\widehat {ABM}\)) và DM = DB (tính chất hai tiếp tuyến cắt nhau).
Suy ra tam giác MBD đều.
Khi đó DB = MB.
Tam giác ABM vuông tại M: \[MB = \sqrt {A{B^2} - A{M^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 \].
Ta có CA = CM và CO là tia phân giác của \(\widehat {ACM}\) (tính chất hai tiếp tuyến cắt nhau).
Suy ra tam giác ACM cân tại C có CO là vừa là đường phân giác, vừa là đường cao.
Gọi K là giao điểm của CO và AM. Suy ra K là trung điểm của AM và CK ⊥ AK.
Ta có \(\widehat {CAK} = 90^\circ - \widehat {KAO} = 90^\circ - 60^\circ = 30^\circ \).
Tam giác AKC vuông tại K: \[AC = \frac{{AK}}{{\cos \widehat {CAK}}} = \frac{{AM}}{{2.\cos \widehat {CAK}}} = \frac{R}{{2.\cos 30^\circ }} = \frac{R}{{\sqrt 3 }}\].
Khi đó \[{S_{ABDC}} = \frac{{\left( {AC + BD} \right).AB}}{2} = \frac{{\left( {AC + MB} \right).AB}}{2}\].
\[ = \frac{{\left( {\frac{R}{{\sqrt 3 }} + R\sqrt 3 } \right).2R}}{2} = \frac{{4{R^2}}}{{\sqrt 3 }}\].
Vậy diện tích tứ giác ABDC bằng \[\frac{{4{R^2}}}{{\sqrt 3 }}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 42,85%.
B. 30%.
C. 70%.
D. 233,33%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.