Cho phương trình sau: x2 + ax + b = 0. Xác định a và b để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: x1 – x2 = 5 và \({x_1}^3 - {x_2}^3 = 35.\) Tìm 2 nghiệm phân biệt đó.
Cho phương trình sau: x2 + ax + b = 0. Xác định a và b để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: x1 – x2 = 5 và \({x_1}^3 - {x_2}^3 = 35.\) Tìm 2 nghiệm phân biệt đó.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Để phương trình có 2 nghiệm phân biệt thì \(\Delta > 0\) ⇔ a2 – 4b > 0
Theo hệ thức Viet, ta có:
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} = - a}\\{{x_1}.{x_2} = b}\end{array}} \right.\)
Ta có: \({x_1}^3 - {x_2}^3 = 35\)
⇔ \(\left( {{x_1} - {x_2}} \right)\left( {{x_1}^2 + {x_1}{x_2} + {x_2}^2} \right) = 35\)
⇔ \(5\left( {{x_1}^2 + {x_1}{x_2} + {x_2}^2} \right) = 35\)
⇔ \({x_1}^2 + {x_1}{x_2} + {x_2}^2 = 7\)
⇔ \({\left( {{x_1} - {x_2}} \right)^2} + 3{x_1}{x_2} = 7\)
⇔ \(25 + 3{x_1}{x_2} = 7\)
⇔ \({x_1}{x_2} = - 6\)
⇔ b = −6
Ta có hệ phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} - {x_2} = 5}\\{{x_1}{x_2} = - 6}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{\left( {5 + {x_2}} \right){x_2} = - 6}\end{array}} \right.\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{{x_2}^2 + 5{x_2} + 6 = 0}\end{array}} \right.\)
⇔ \(\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{\left( {{x_2} + 2} \right)\left( {{x_2} + 3} \right) = 0}\end{array}} \right.\)
⇔ \(\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{{x_2} + 2 = 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 5 + {x_2}}\\{{x_2} + 3 = 0}\end{array}} \right.}\end{array}} \right.\) ⇔ \(\left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 3}\\{{x_2} = - 2}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{{x_1} = 2}\\{{x_2} = - 3}\end{array}} \right.}\end{array}} \right.\)
TH1: x1 = 3 và x2 = −2 ⇒ x1 + x2 = 1 = a
⇒ \(\left\{ {\begin{array}{*{20}{c}}{a = 1}\\{b = - 6}\end{array}} \right.\)
TH2: x1 = 2 và x2 = −3 ⇒ x1 + x2 = −1 = a
⇒ \(\left\{ {\begin{array}{*{20}{c}}{a = - 1}\\{b = - 6}\end{array}} \right.\)
Vậy các cặp (a,b) thỏa mãn là (1,−6) hoặc (−1,−6).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
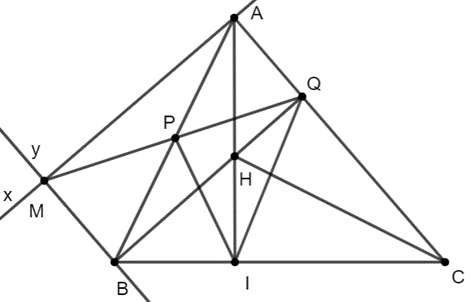
Vì Ax ⊥ AC ⇒ AM ⊥ AC
mà BM // AC
⇒ AM ⊥ BM
Chứng minh tương tự ⇒ AQ // BM và BM // AQ (cmt)
Suy ra AMBQ là hình bình hành.
Mà \(\widehat {AMB} = \widehat {MBQ} = \widehat {ABQ} = \widehat {MAQ} = {90^o}\).
Vậy AMBQ là hình chữ nhật.
b) BQ ⊥ AC (cmt) mà \(BQ \cap AI = H\)
Suy ra H là trực tâm của tam giác ABC.
Do đó: CH ⊥ AB
c) AMBQ là hình chữ nhật mà \(AB \cap QM = P\)
⇒ P là trung điểm AB và P là trung điểm QM
\(\Delta ABI\) vuông tại I có đường trung tuyến IP
⇒ \(IP = \frac{1}{2}AB\)
⇒ IP = PQ
⇒ \(\Delta IPQ\) cân tại P.
Lời giải
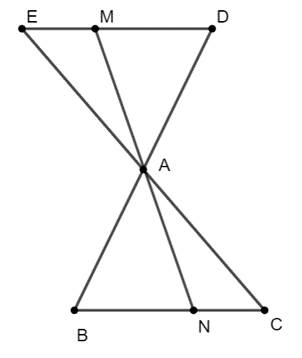
a) Xét \(\Delta ADE\) và \(\Delta ABC\) có:
AD = AB
\(\widehat {DAE} = \widehat {BAC}\) (2 góc đối đỉnh)
AC = AE
⇒ \(\Delta ADE = \Delta BAC\left( {c.g.c} \right)\)
⇒ \(\widehat {ADE} = \widehat {ABC}\) (2 góc tương ứng) mà chúng ở vị trí so le trong với nhau
⇒ BC // DE (đpcm)
b) Xét \(\Delta DAM\) và \(\Delta BAN\) có:
\(\widehat {DAM} = \widehat {BAN}\) (2 góc đối đỉnh)
AD = AB
\(\widehat {ABN} = \widehat {ADM}\) (CMT)
⇒ \(\Delta DAM = \Delta BAN\left( {g.c.g} \right)\)
⇒ AM = AN (2 cạnh tương ứng) (dpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. −8;
B. \(3\sqrt {11} - 13\);
C. −39;
D. −21.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.