Câu hỏi:
03/07/2023 5,968
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1) Chứng minh: SD là tiếp tuyến của đường tròn (O).
2) Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3) Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH\,.\,KD\).
Cho đường tròn (O; R) có đường kính AB, lấy điểm M thuộc đường tròn (O) sao cho AM < MB. Tiếp tuyến tại A của đường tròn (O) cắt tia OM tại S. Đường cao AH của tam giác SAO (H thuộc SO) cắt đường tròn (O) tại D.
1) Chứng minh: SD là tiếp tuyến của đường tròn (O).
2) Kẻ đường kính DE của đường tròn (O). Gọi r là bán kính đường tròn nội tiếp tam giác SAD. Chứng minh M là tâm đường tròn nội tiếp tam giác SAD và tính độ dài đoạn thẳng AE theo R và r.
3) Cho AM = r. Gọi K là giao điểm của BM và AD. Chứng minh: \(\frac{{M{D^2}}}{6} = KH\,.\,KD\).
Câu hỏi trong đề:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
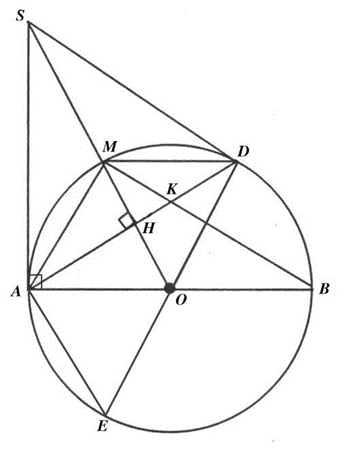
1) Xét ∆OAB có \(\left\{ \begin{array}{l}OA = OD = R\\OH \bot AD\end{array} \right.\)
Þ ∆OAD cân tại O có OH là đường cao
Þ OH là đường phân giác của \(\widehat {AOD}\)
\[ \Rightarrow \widehat {AOH} = \widehat {DOH}\]hay\[\widehat {AOS} = \widehat {DOS}\]
Xét ∆SAO và ∆SDO có:
KO chung
\[\widehat {AOS} = \widehat {DOS}\]
OA = OD = R
Do đó ∆SAO = ∆SDO (c.g.c)
Mà \(\widehat {SAO} = 90^\circ \) (SA ^ OA do SA là tiếp tuyến của (O) tại A)
\( \Rightarrow \widehat {SDO} = 90^\circ \)hay SD ^ OD
Suy ra SD là tiếp tuyến của (O) tại D.
2) ∆OAM có OA = OM = R
Þ ∆OAM cân tại O \( \Rightarrow \widehat {OAM} = \widehat {OMA}\)
Mà \[\widehat {OAM} + \widehat {SAM} = \widehat {SAO} = 90^\circ \] và \[\widehat {AMH} + \widehat {HAM} = 90^\circ \] (∆HAM vuông tại H)
\( \Rightarrow \widehat {SAM} = \widehat {HAM}\)
Þ AM là đường phân giác của ∆SAD (1)
Mặt khác SA, SD là các tiếp tuyến của đường tròn (O)
Þ SO là tia phân giác của \[\widehat {ASD}\]
Þ SO là đường phân giác của ∆SAD (2)
Từ (1) và (2) Þ M là tâm đường tròn nội tiếp ∆SAD
Mà MH ^ AD tại H Þ MH là bán kính đường tròn nội tiếp ∆SAD
Þ MH = r Þ OH = R − r
Áp dụng định lí Py-ta-go vào ∆AOH vuông tại H, ta có:
\(AH = \sqrt {O{A^2} - O{H^2}} = \sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \)
\[ \Rightarrow AD = 2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} \]
Ta có \(\widehat {EAD}\) chắn đường kính DE suy ra \[\widehat {EAD} = 90^\circ \].
Áp dụng định lí Py-ta-go vào ∆EAD vuông tại A, ta có:
\(AE = \sqrt {D{E^2} - A{D^2}} = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {2\sqrt {{R^2} - {{\left( {R - r} \right)}^2}} } \right)}^2}} = 2\left( {R - r} \right)\)
3) OH là đường trung trực của AD, M Î OH Þ DM = AM = R
Tứ giác AMDO có AM = MD = OA = OD (=R)
ÞTứ giác AMDO là hình thoi
ÞAM // OD. Mà AM ^ BMÞ BM ^ OD
∆OMD có OM = OD = CD (=R) Þ ∆OMD đều
Mà MB, DM là hai đường cao cắt nhau tại K của ∆OMD
Do đó K là trực tâm của tam giác đều OMD
Þ K là trọng tâm của tam giác đều OMD
\[ \Rightarrow KH = \frac{1}{3}DH,\;KD = \frac{2}{3}DH \Rightarrow KH\,.\,KD = \frac{2}{9}D{H^2}\]
Mà ∆HMD vuông tại H
\[ \Rightarrow DH = MD\,.\,\sin \widehat {HMD} = MD\,.\,\sin 60^\circ = \frac{{\sqrt 3 }}{2}MD\]
\( \Rightarrow MD = \frac{2}{{\sqrt 3 }}DH\)
\( \Rightarrow M{D^2} = \frac{4}{3}D{H^2} = 6\,.\,\frac{2}{9}D{H^2} = 6KH\,.\,KD\)
\( \Rightarrow \frac{{M{D^2}}}{6} = KH\,.\,KD\).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1,2,3.
Có bao nhiêu số gồm 5 chữ số phân biệt có mặt đủ ba chữ số 1,2,3.
Xem đáp án »
03/07/2023
14,685
Câu 2:
Cho B=3 + 32 + 33 + ... + 3120. Chứng minh:
a) B chia hết cho 3;
b) B chia hết cho 4;
c) B chia hết cho 13.
Cho B=3 + 32 + 33 + ... + 3120. Chứng minh:
a) B chia hết cho 3;
b) B chia hết cho 4;
c) B chia hết cho 13.
Xem đáp án »
03/07/2023
5,683
Câu 3:
Tam giác ABC vuông tại A, AB = a, AC = 3a.Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Chứng minh \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\).
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách.
Tam giác ABC vuông tại A, AB = a, AC = 3a.Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Chứng minh \(\frac{{DE}}{{DB}} = \frac{{DB}}{{DC}}\).
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính tổng \(\widehat {AEB} + \widehat {BCD}\) bằng hai cách.
Xem đáp án »
03/07/2023
5,363
Câu 4:
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.
a) Chứng minh CD = AC + BD.
b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. CM: AF.BC = KE.EB.
c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.
d) EA cắt CF tại M. EB cắt DF tại N. CM: M, I, N thẳng hàng.
Cho đường tròn (O; R) có đường kính AB. Vẽ các tiếp tuyến Ax, By của đường tròn (O), trên đường tròn (O) lấy một điểm E bất kì (E khác A, B). Tiếp tuyến tại E của đường tròn (O) cắt Ax, By lần lượt tại C, D.
a) Chứng minh CD = AC + BD.
b) Vẽ EF vuông góc AB tại F, BE cắt AC tại K. CM: AF.BC = KE.EB.
c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.
d) EA cắt CF tại M. EB cắt DF tại N. CM: M, I, N thẳng hàng.
Xem đáp án »
03/07/2023
3,609
Câu 5:
Cho hình chóp S.ABCD có AD và BC không song song. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của (SAD) và (SBC).
b) Chứng minh MN // (ABCD).
c) Tìm giao điểm của đường thẳng SD với (AMN).
Cho hình chóp S.ABCD có AD và BC không song song. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của (SAD) và (SBC).
b) Chứng minh MN // (ABCD).
c) Tìm giao điểm của đường thẳng SD với (AMN).
Xem đáp án »
03/07/2023
3,409
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho 3 điểm A(−4; 1), B(2; 4), C(2; −2).
a) Tìm tọa độ trọng tâm của tam giác ABC.
b) Tìm tọa độ điểm D sao cho C là trọng tâm của tam giác ABD.
c) Tìm tọa độ điểm E sao cho tứ giác ABCE là hình bình hành.
Trong mặt phẳng tọa độ Oxy, cho 3 điểm A(−4; 1), B(2; 4), C(2; −2).
a) Tìm tọa độ trọng tâm của tam giác ABC.
b) Tìm tọa độ điểm D sao cho C là trọng tâm của tam giác ABD.
c) Tìm tọa độ điểm E sao cho tứ giác ABCE là hình bình hành.
Xem đáp án »
03/07/2023
3,346
về câu hỏi!