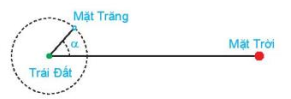
Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là α (0° ≤ α ≤ 360°) thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bởi công thức

\(F = \frac{1}{2}\left( {1 - \cos \alpha } \right)\).

(Theo trang usno.navy.mil).

Xác định góc α tương ứng với các pha sau của Mặt Trăng:

a) F = 0 (trăng mới);

b) F = 0,25 (trăng lưỡi liềm);

c) F = 0,5 (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng);

d) F = 1 (trăng tròn).

Lời giải:

Vị trí cân bằng của vật dao động điều hòa là vị trí vật đứng yên, khi đó x = 0, ta có

\(2\cos \left( {5t - \frac{\pi }{6}} \right) = 0\)

\( \Leftrightarrow \cos \left( {5t - \frac{\pi }{6}} \right) = 0\)

\( \Leftrightarrow 5t - \frac{\pi }{6} = \frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}\)

\( \Leftrightarrow t = \frac{{2\pi }}{{15}} + k\frac{\pi }{5},\,\,k \in \mathbb{Z}\)

Trong khoảng thời gian từ 0 đến 6 giây, tức là 0 ≤ t ≤ 6 hay \(0 \le \frac{{2\pi }}{{15}} + k\frac{\pi }{5} \le 6\)

\( \Leftrightarrow - \frac{2}{3} \le k \le \frac{{90 - 2\pi }}{{3\pi }}\)

Vì k ∈ ℤ nên k ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8}.

Vậy trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng 9 lần.

Lời giải:

Vì v₀ = 500 m/s, g = 9,8 m/s² nên ta có phương trình quỹ đạo của quả đạn là

\(y = \frac{{ - 9,8}}{{{{2.500}^2}.{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) hay \(y = \frac{{ - 49}}{{2\,500\,000{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \).

a) Quả đạn chạm đất khi y = 0, khi đó \(\frac{{ - 49}}{{2\,500\,000{{\cos }^2}\alpha }}{x^2} + x\tan \alpha = 0\)

\( \Leftrightarrow x\left( {\frac{{ - 49}}{{2\,500\,000{{\cos }^2}\alpha }}x + \tan \alpha } \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{2\,500\,000{{\cos }^2}\alpha .\tan \alpha }}{{49}}\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{2\,500\,000\cos \alpha .\sin \alpha }}{{49}}\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{1\,250\,000\sin 2\alpha }}{{49}}\end{array} \right.\)

Loại x = 0 (đạn pháo chưa được bắn).

Vậy tầm xa mà quả đạn đạt tới là \(x = \frac{{1250000\sin 2\alpha }}{{49}}\) (m).

b) Để quả đạn trúng mục tiêu cách vị trí đặt khẩu pháo 22 000 m thì x = 22 000 m.

Khi đó \(\frac{{1250000\sin 2\alpha }}{{49}} = 22\,000\)⇔ sin 2α = \(\frac{{539}}{{625}}\)

\[ \Leftrightarrow \left[ \begin{array}{l}\alpha \approx 29^\circ 47'36''\\\alpha \approx 60^\circ 12'23''\end{array} \right.\,\,\].

c) Hàm số \(y = \frac{{ - 49}}{{2\,500\,000{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) là một hàm số bậc hai có đồ thị là một parabol có tọa độ đỉnh I(x_I; y_I) là

\(\left\{ \begin{array}{l}{x_I} = - \frac{b}{{2a}} = - \frac{{\tan \alpha }}{{2.\frac{{ - 49}}{{2\,500\,000{{\cos }^2}\alpha }}}} = \frac{{1\,250\,\,000\cos \alpha \sin \alpha }}{{49}}\\{y_I} = f\left( {{x_I}} \right) = \frac{{ - 49}}{{2\,500\,000{{\cos }^2}\alpha }}{\left( {\frac{{1\,250\,\,000\cos \alpha \sin \alpha }}{{49}}} \right)^2} + \frac{{1\,250\,\,000\cos \alpha \sin \alpha }}{{49}}\tan \alpha \end{array} \right.\)

Hay \(\left\{ \begin{array}{l}{x_I} = \frac{{1\,250\,\,000\cos \alpha \sin \alpha }}{{49}}\\{y_I} = \frac{{625\,\,000{{\sin }^2}\alpha }}{{49}}\end{array} \right.\)

Do đó, độ cao lớn nhất của quả đạn là \({y_{\max }} = \frac{{625\,\,000{{\sin }^2}\alpha }}{{49}}\).

Ta có \({y_{\max }} = \frac{{625\,\,000{{\sin }^2}\alpha }}{{49}} \le \frac{{625\,000}}{{49}}\), dấu “=” xảy ra khi sin² α = 1 hay α = 90°.

Như vậy góc bắn α = 90° thì quả đan đạt độ cao lớn nhất.