Giải SGK Toán 11 KNTT Bài 4. Phương trình lượng giác cơ bản có đáp án
25 người thi tuần này 4.6 1.6 K lượt thi 17 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Lời giải:
Sau bài học này ta sẽ giải quyết được bài toán trên như sau:
Chọn hệ trục tọa độ có gốc tọa độ đặt tại vị trí khẩu pháo, trục Ox theo hướng khẩu pháo như hình dưới đây.
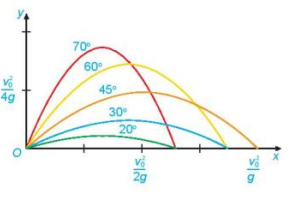
Khi đó theo Vật lí, ta biết rằng quỹ đạo của quả đạn pháo có dạng đường parabol có phương trình \(y = \frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha \) (với g là gia tốc trọng trường).
Cho y = 0 ta được \(\frac{{ - g}}{{2v_0^2{{\cos }^2}\alpha }}{x^2} + x\tan \alpha = 0\), suy ra x = 0 hoặc \(x = \frac{{v_0^2\sin 2\alpha }}{g}\).
Quả đạn tiếp đất khi \(x = \frac{{v_0^2\sin 2\alpha }}{g}\).
Ta có \(x = \frac{{v_0^2\sin 2\alpha }}{g} \le \frac{{v_0^2}}{g}\), dấu bằng xảy ra khi sin 2α = 1.
Giải phương trình sin 2α = 1, ta được α = \(\frac{\pi }{4} + k\pi ,\,\,k \in \mathbb{Z}\).
Do \(0 \le \alpha \le \frac{\pi }{2}\) nên \(\alpha = \frac{\pi }{4}\) hay α = 45°.
Vậy quả đạn pháo sẽ bay xa nhất khi góc bắn bằng 45°.
Lời giải
Lời giải:
+) Ta có: 2x – 4 = 0, suy ra x = 2.
Vậy tập nghiệm của phương trình 2x – 4 = 0 là S1 = {2}.
+) Ta có: (x – 2)(x2 + 1) = 0
Vì x2 ≥ 0 với mọi x ∈ ℝ nên x2 + 1 > 0 với mọi x ∈ ℝ.
Do đó, (x – 2)(x2 + 1) = 0 khi x – 2 = 0 hay x = 2.
Vậy tập nghiệm của phương trình (x – 2)(x2 + 1) = 0 là S2 = {2}.
+) Nhận thấy S1 = S2 = {2}. Vậy hai phương trình đã cho có cùng tập nghiệm.
Lời giải
Lời giải:
+) Ta có: \(\frac{{x - 1}}{{x + 1}} = 0\), điều kiện x ≠ – 1.
Khi đó, \(\frac{{x - 1}}{{x + 1}} = 0\) khi x – 1 = 0 hay x = 1 (thỏa mãn).
Vậy tập nghiệm của phương trình \(\frac{{x - 1}}{{x + 1}} = 0\) là S1 = {1}.
+) Phương trình x2 – 1 = 0 được viết lại thành (x – 1)(x + 1) = 0, từ đó ta tìm được x = 1 hoặc x = – 1, do đó tập nghiệm của phương trình x2 – 1 = 0 là S2 = {– 1; 1}.
+) Nhận thấy S1 ≠ S2, vậy hai phương trình đã cho không tương đương.
Lời giải
Lời giải:
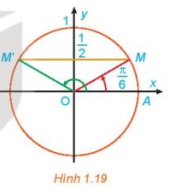
a) Từ Hình 1.19, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc \(\frac{\pi }{6}\) và \(\pi - \frac{\pi }{6} = \frac{{5\pi }}{6}\), lại có tung độ của điểm M và M' đều bằng \(\frac{1}{2}\) nên theo định nghĩa giá trị lượng giác, ta có \(\sin \frac{\pi }{6} = \frac{1}{2}\) và \(\sin \frac{{5\pi }}{6} = \frac{1}{2}\).
Vậy trong nửa khoảng [0; 2π), phương trình \(\sin x = \frac{1}{2}\) có hai nghiệm là \(x = \frac{\pi }{6}\), \(x = \frac{{5\pi }}{6}\).
b) Vì hàm số sin có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là \(x = \frac{\pi }{6} + k2\pi ,\,k \in \mathbb{Z}\) và \(x = \frac{{5\pi }}{6} + k2\pi ,\,k \in \mathbb{Z}\).
Lời giải
Lời giải:
a) \(\sin x = \frac{{\sqrt 2 }}{2}\)
\( \Leftrightarrow \sin x = \sin \frac{\pi }{4}\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{{3\pi }}{4} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình \(\sin x = \frac{{\sqrt 2 }}{2}\) có các nghiệm là \(x = \frac{\pi }{4} + k2\pi ,\,\,k \in \mathbb{Z}\) và \(x = \frac{{3\pi }}{4} + k2\pi \), \(k \in \mathbb{Z}\).
b) sin 3x = – sin 5x
⇔ sin 3x = sin (– 5x)
\( \Leftrightarrow \left[ \begin{array}{l}3x = - 5x + k2\pi \\3x = \pi - \left( { - 5x} \right) + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}3x = - 5x + k2\pi \\3x = \pi + 5x + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}8x = k2\pi \\ - 2x = \pi + k2\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow \left[ \begin{array}{l}x = k\frac{\pi }{4}\\x = - \frac{\pi }{2} + k\pi \end{array} \right.\,\left( {k \in \mathbb{Z}} \right)\)
Vậy phương trình đã cho có các nghiệm là \(x = k\frac{\pi }{4},\,k \in \mathbb{Z}\) và \(x = - \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.