Câu hỏi:
13/07/2024 6,249
Guồng nước (hay còn gọi là cọn nước) không chỉ là công cụ phục vụ sản xuất nông nghiệp, mà đã trở thành hình ảnh quen thuộc của bản làng và là một nét văn hoá đặc trưng của đồng bào dân tộc miền núi phía Bắc.
Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m. Khi guồng quay đều, khoảng cách h (m) từ một ống đựng nước gắn tại một điểm của guồng đến mặt nước được tính theo công thức h = |y|, trong đó \(y = 2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2\), với x (phút) là thời gian quay của guồng (x ≥ 0).
(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020).
Khoảng cách h phụ thuộc vào thời gian quay x như thế nào?
Guồng nước (hay còn gọi là cọn nước) không chỉ là công cụ phục vụ sản xuất nông nghiệp, mà đã trở thành hình ảnh quen thuộc của bản làng và là một nét văn hoá đặc trưng của đồng bào dân tộc miền núi phía Bắc.
Một chiếc guồng nước có dạng hình tròn bán kính 2,5 m; trục của nó đặt cách mặt nước 2 m. Khi guồng quay đều, khoảng cách h (m) từ một ống đựng nước gắn tại một điểm của guồng đến mặt nước được tính theo công thức h = |y|, trong đó \(y = 2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2\), với x (phút) là thời gian quay của guồng (x ≥ 0).
(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020).
Khoảng cách h phụ thuộc vào thời gian quay x như thế nào?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Với x ≥ 0, xét hàm số \[y = 2,5\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2\]
\[ = - 2,5\sin \left( {\frac{\pi }{2} - 2\pi x} \right) + 2\]
\[ = - 2,5\cos \left( {2\pi x} \right) + 2\]
Khi đó h = |y| = |‒2,5cos2πx + 2|.
Vậy khoảng cách h phụ thuộc vào thời gian quay x theo công thức h = |‒2,5cos2πx + 2|.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Xét hàm số f(x) = y = sinx cosx có tập xác định D = ℝ:
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = sin(‒x) . cos(‒x) = ‒sinx cosx = ‒f(x).
Do đó hàm số y = sinx cosx là hàm số lẻ.
b) Xét hàm số f(x) = y = tanx + cotx có tập xác định \(D = \mathbb{R}\backslash \left\{ {k\pi ;\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\):
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = tan(‒x) + cot(‒x) = (‒tanx) + (‒cotx) = ‒(tanx + cotx) = ‒f(x).
Do đó hàm số y = tanx + cotx là hàm số lẻ.
c) Xét hàm số f(x) = y = sin2x có tập xác định D = ℝ:
• ∀x ∈ D thì ‒x ∈ D;
• f(‒x) = sin2(‒x) = (‒sinx)2 = sin2x = f(x).
Do đó hàm số y = sin2x là hàm số chẵn.
Lời giải
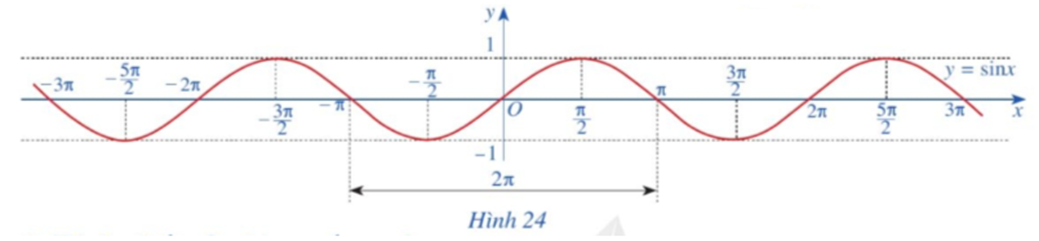
Quan sát đồ thị hàm số y = sinx ta thấy:
• Hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{{5\pi }}{2}; - \frac{{3\pi }}{2}} \right);\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right);\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right);...\)
Ta có: \(\left( { - \frac{{5\pi }}{2}; - \frac{{3\pi }}{2}} \right) = \left( { - \frac{\pi }{2} - 2\pi ;\frac{\pi }{2} - 2\pi } \right)\);
\[\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right) = \left( { - \frac{\pi }{2} + 2\pi ;\frac{\pi }{2} + 2\pi } \right)\];
…
Do đó ta có thể viết hàm số đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) với k ∈ ℤ.
• Hàm số nghịch biến trên mỗi khoảng \(\left( { - \frac{{7\pi }}{2}; - \frac{{5\pi }}{2}} \right);\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right);\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right);...\)
Ta có: \[\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right) = \left( {\frac{\pi }{2} - 2\pi ;\frac{{3\pi }}{2} - 2\pi } \right)\];
…
Do đó ta có thể viết hàm số nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với k ∈ ℤ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
Bài tập Tổ hợp - Xác suất cơ bản, nâng cao có lời giải chi tiết (P6)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận