Giải SGK Toán 11 Cánh Diều Bài tập cuối chương 1 có đáp án

Đáp án đúng là: C

Cách 1. Dựa vào đồ thị hàm số:

 Đồ thị hàm số y = sinx (hình vẽ):

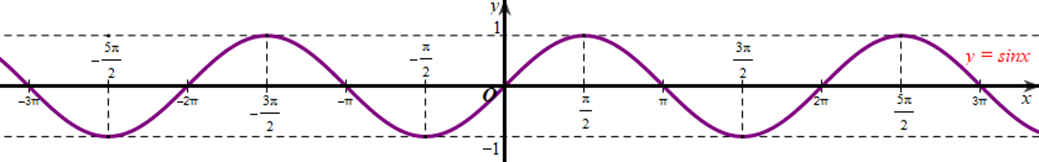
Quan sát đồ thị trên, ta thấy hàm số y = sinx đồng biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).

Cách 2. Dùng tính chất của hàm số y = sinx:

Hàm số y = sinx đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) với k ∈ ℤ.

Do đó hàm số y = sinx đồng biến trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).

Đáp án đúng là: D

Cách 1. Dùng đồ thị hàm số:

Xét đồ thị hàm số y = sinx:

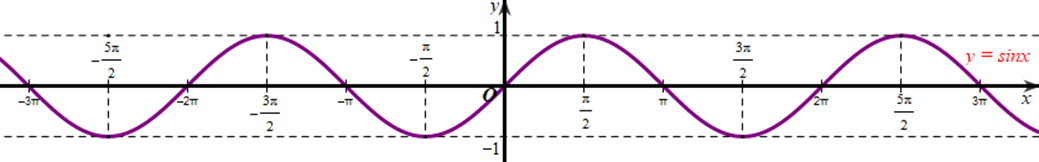
Xét đồ thị hàm số y = cosx:

Xét đồ thị hàm số y = tanx:

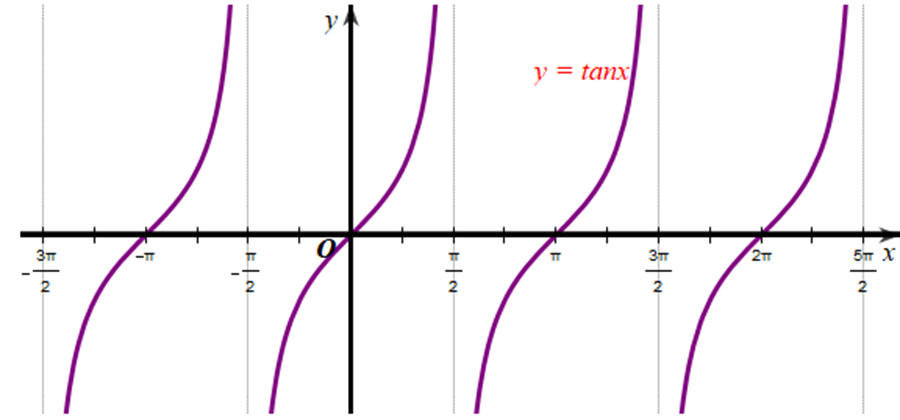
Xét đồ thị hàm số y = cotx:

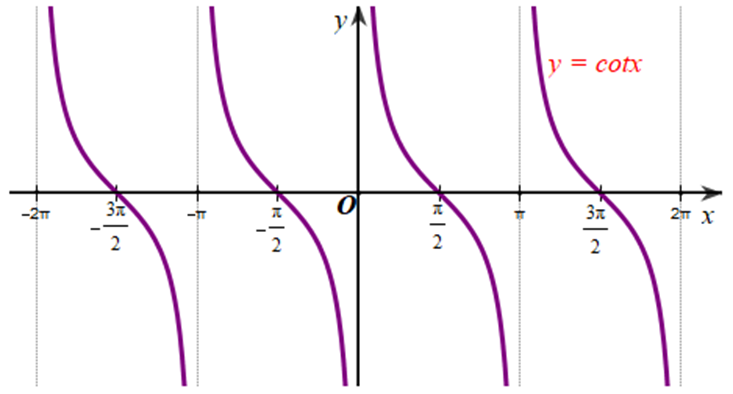
Quan sát các đồ thị trên, ta thấy hàm số y = cotx nghịch biến trên khoảng (π; 2π).

Cách 2. Dùng tính chất của hàm số lượng giác:

Do (π; 2π) = (0 + π; π + π)

Mà hàm số y = cotx nghịch biến trên mỗi khoảng (kπ; π + kπ) với k ∈ ℤ.

Do đó hàm số y = cotx nghịch biến trên khoảng (π; 2π).

Đáp án đúng là: A

Ta có: tan2a = tan[(a + b) + (a – b)]

                    \( = \frac{{\tan \left( {a + b} \right) + \tan \left( {a - b} \right)}}{{1 - \tan \left( {a + b} \right)\tan \left( {a - b} \right)}} = \frac{{3 + \left( { - 3} \right)}}{{1 - 3.\left( { - 3} \right)}} = 0\).

Đáp án đúng là: B

Ta có: cos2a = 2cos²a – 1 = \(2.{\left( {\frac{1}{4}} \right)^2} - 1 = 2.\frac{1}{{16}} - 1 = - \frac{7}{8}\).

Đáp án đúng là: A

Áp dụng công thức biến đổi tích thành tổng, ta có:

\[cos\left( {a + b} \right)cos\left( {a--b} \right) = \frac{1}{2}\left[ {\cos \left( {a + b + a - b} \right) + \cos \left( {a + b - a + b} \right)} \right]\]

                                  \[ = \frac{1}{2}\left[ {\cos 2a + \cos 2b} \right]\]

Ta lại có:

cos2a = 2cos²a – 1 = \(2.{\left( {\frac{3}{5}} \right)^2} - 1 = 2.\frac{9}{{25}} - 1 = - \frac{7}{{25}}\);

cos2b = 2cos²b – 1 = \(2.{\left( { - \frac{4}{5}} \right)^2} - 1 = 2.\frac{{16}}{{25}} - 1 = \frac{7}{{25}}\);

Do đó \[cos\left( {a + b} \right)cos\left( {a--b} \right) = \frac{1}{2}\left[ {\cos 2a + \cos 2b} \right] = \frac{1}{2}.\left( { - \frac{7}{{25}} + \frac{7}{{25}}} \right) = 0\].

Đáp án đúng là: C

Áp dụng công thức biến đổi tổng thành tích, ta có:

\(\sin \left( {a + \frac{\pi }{4}} \right) + \sin \left( {a - \frac{\pi }{4}} \right)\)

\( = 2\sin \left( {\frac{{a + \frac{\pi }{4} + a - \frac{\pi }{4}}}{2}} \right)\cos \left( {\frac{{a + \frac{\pi }{4} - a + \frac{\pi }{4}}}{2}} \right)\)

\( = 2\sin a\cos \frac{\pi }{4} = 2.\left( { - \frac{{\sqrt 2 }}{3}} \right).\frac{{\sqrt 2 }}{2} = - \frac{2}{3}\).

Đáp án đúng là: C

Cách 1. Giải phương trình lượng giác

cosx = 0

\( \Leftrightarrow x = \frac{\pi }{2} + k\pi \,\,\,\left( {k \in \mathbb{Z}} \right)\)

Do x ∈ [0; 10π] nên ta có: \[0 \le \frac{\pi }{2} + k\pi \, \le 10\pi \]

\[ \Leftrightarrow 0 \le \frac{1}{2} + k \le 10 \Leftrightarrow - \frac{1}{2} \le k \le \frac{{19}}{2}\]

Mà k ∈ ℤ nên k ∈ {0; 1; 2; …; 9}, khi đó ta tìm được 10 giá trị của x.

Vậy phương trình cosx = 0 có 10 nghiệm trên đoạn [0; 10π].

Cách 2. Dùng đồ thị hàm số

Quan sát đồ thị ta thấy đồ thị hàm số y = cosx cắt trục hoành tại 10 điểm A, B, C, …, K trên đoạn [0; 10π].

Vậy phương trình cosx = 0 có 10 nghiệm trên đoạn [0; 10π].

Đáp án đúng là: D

Cách 1. Giải phương trình lượng giác

sinx = 0

Û x = kπ (k ∈ ℤ)

Do x ∈ [0; 10π] nên ta có: 0 ≤ kπ ≤ 10π

Û 0 ≤ k ≤ 10

Mà k ∈ ℤ nên k ∈ {0; 1; 2; …; 10}, khi đó ta tìm được 11 giá trị của x.

Vậy phương trình sinx = 0 có 11 nghiệm trên đoạn [0; 10π].

Cách 2. Dùng đồ thị hàm số

Quan sát đồ thị ta thấy đồ thị hàm số y = sinx cắt trục hoành tại 11 điểm A ≡ O, B, C, …, M trên đoạn [0; 10π].

Vậy phương trình sinx = 0 có 11 nghiệm trên đoạn [0; 10π].