Câu hỏi:
13/07/2024 566Hằng ngày, mực nước của một con kênh lên xuống theo thuỷ triều. Độ sâu h(m) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày (0 ≤ t < 24) cho bởi công thức \(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12\) (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2021). Tìm t để độ sâu của mực nước là:
10,5 m.
Sách mới 2k7: 30 đề đánh giá năng lực DHQG Hà Nội, Tp. Hồ Chí Minh, BKHN 2025 mới nhất (600 trang - chỉ từ 160k).
Quảng cáo
Trả lời:
Để độ sâu của mực nước là 10,5 m thì:
\(h = 3\cos \left( {\frac{{\pi t}}{6} + 1} \right) + 12 = 10,5\)
\[ \Leftrightarrow \cos \left( {\frac{{\pi t}}{6} + 1} \right) = - \frac{1}{2}\]
\[ \Leftrightarrow \left[ \begin{array}{l}\frac{{\pi t}}{6} + 1 = \frac{{2\pi }}{3} + k2\pi \\\frac{{\pi t}}{6} + 1 = - \frac{{2\pi }}{3} + k2\pi \,\,\,\end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
\[ \Leftrightarrow \left[ \begin{array}{l}t = 4 - \frac{6}{\pi } + 12k\,\,\,\,\,\left( 1 \right)\\t = - 4 - \frac{6}{\pi } + 12k\,\,\,\left( 2 \right)\,\,\,\end{array} \right.\left( {k \in \mathbb{Z}} \right)\]
• Do 0 ≤ t < 24 nên từ (1) ta có: \(0 \le 4 - \frac{6}{\pi } + 12k < 24\)
\( \Leftrightarrow - 4 + \frac{6}{\pi } \le 12k < 20 + \frac{6}{\pi }\)
\( \Leftrightarrow - \frac{1}{3} + \frac{1}{{2\pi }} \le k < \frac{5}{3} + \frac{1}{{2\pi }}\)
Mà k ∈ ℤ nên k ∈ {0; 1}.
Với k = 0 thì \(t = 4 - \frac{6}{\pi } + 12.0 \approx 2,09\) (giờ);
Với k = 1 thì \(t = 4 - \frac{6}{\pi } + 12.1 \approx 14,09\) (giờ).
• Do 0 ≤ t < 24 nên từ (2) ta có: \(0 \le - 4 - \frac{6}{\pi } + 12k < 24\)
\( \Leftrightarrow 4 + \frac{6}{\pi } \le 12k < 28 + \frac{6}{\pi }\)
\( \Leftrightarrow \frac{1}{3} + \frac{1}{{2\pi }} \le k < \frac{7}{3} + \frac{1}{{2\pi }}\)
Mà k ∈ ℤ nên k ∈ {1; 2}.
Với k = 1 thì \(t = - 4 - \frac{6}{\pi } + 12.1 \approx 6,09\) (giờ);
Với k = 2 thì \(t = - 4 - \frac{6}{\pi } + 12.2 \approx 18,09\) (giờ).
Vậy lúc 2,09 giờ, 6,09 giờ, 14,09 giờ và 18,09 giờ thì mực nước có độ sâu là 10,5 m.
Đã bán 152
Đã bán 114
Đã bán 132
Đã bán 47
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Vẽ đồ thị hàm số y = cosx trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) rồi xác định số nghiệm của phương trình 3cosx + 2 = 0 trên đoạn đó.
Câu 2:
Nếu tan(a + b) = 3, tan(a – b) = ‒3 thì tan2a bằng:
A. 0.
B. \(\frac{3}{5}\).
C. 1.
D. \( - \frac{3}{4}\).
Câu 3:
Nếu \(\cos a = \frac{1}{4}\) thì cos2a bằng:
A. \(\frac{7}{8}\).
B. \( - \frac{7}{8}\).
C. \(\frac{{15}}{{16}}\).
D. \( - \frac{{15}}{{16}}\).
Câu 4:
Nếu \(\cos a = \frac{3}{5}\) và \(\cos b = - \frac{4}{5}\) thì cos(a + b)cos(a – b) bằng:
A. 0.
B. 2.
C. 4.
D. 5.
Câu 5:
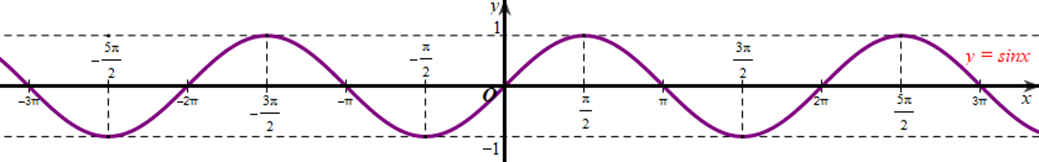
Hàm số y = sinx đồng biến trên khoảng:
A. (0; π).
B. \(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
C. \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).
Câu 6:
Số nghiệm của phương trình cosx = 0 trên đoạn [0; 10π] là:
D. 11.
Câu 7:
Hàm số nghịch biến trên khoảng (π; 2π) là:
A. y = sinx.
B. y = cosx.
C. y = tanx.
D. y = cotx.
về câu hỏi!