Giải SGK Toán 11 Cánh Diều Các phép biến đổi lượng giác có đáp án

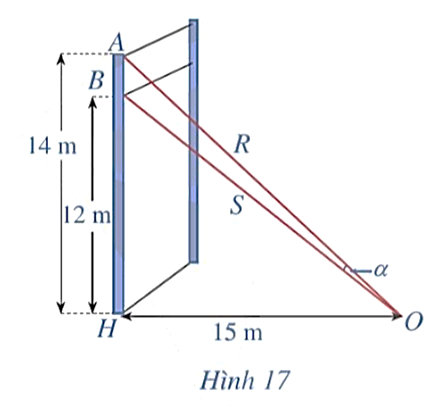
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Có các công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác sau:

‒ Công thức cộng;

‒ Công thức nhân đôi;

‒ Công thức biến đổi tích thành tổng;

‒ Công thức biến đổi tổng thành tích.

Với \(a = \frac{\pi }{6}\) ta có \[\sin a = \sin \frac{\pi }{6} = \frac{1}{2}\]; \(\cos a = \cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\).

Với \(b = \frac{\pi }{3}\) ta có \[\sin b = \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\]; \(\cos b = \cos \frac{\pi }{3} = \frac{1}{2}\).

Ta có \(\sin \left( {a + b} \right) = \sin \left( {\frac{\pi }{6} + \frac{\pi }{3}} \right) = \sin \frac{\pi }{2} = 1\);

          \[\sin a\cos b + \cos a\sin b = \frac{1}{2}.\frac{1}{2} + \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} = \frac{1}{4} + \frac{3}{4} = 1\]

Do đó sin(a + b) = sina cosb + cosa sinb (vì cùng bằng 1).

Ta có sin(a – b) = sin[a + (‒b)]

                          = sina cos(‒b) + cosa sin(‒b)

                          = sina cosb + cosa (‒sinb)

                          = sina cosb ‒ cosa sinb

Áp dụng công thức cộng ta có:

\[\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right) = \sin \frac{\pi }{3}\cos \frac{\pi }{4} - \cos \frac{\pi }{3}\sin \frac{\pi }{4}\]

\( = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} - \frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 6 - \sqrt 2 }}{4}\).

Ta có: cos(a + b) = \(\sin \left[ {\frac{\pi }{2} - \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right]\)

               \( = \sin \left( {\frac{\pi }{2} - a} \right).\cos b - c{\rm{os}}\left( {\frac{\pi }{2} - a} \right).\sin b\)

               \( = \cos a.\cos b - \sin a.\sin b\)

Vậy cos(a + b) = cosa cosb – sina sinb.

Ta có: cos(a – b) = cos[a + (‒b)]

             = cosa cos(‒b) – sina sin(‒b)

             = cosa cosb ‒ sina (‒sinb)

             = cosa cosb + sina sinb.

Vậy cos(a – b) = cosa cosb + sina sinb.

Áp dụng công thức cộng, ta có:

cos15° = cos(45° ‒ 30°)

            = cos45°.cos30° + sin45°.sin30°

            \( = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\).

Khi các biểu thức đều có nghĩa, ta có:

tan(a + b) \( = \frac{{\sin \left( {a + b} \right)}}{{cos\left( {a + b} \right)}} = \frac{{\sin a\cos b + \cos a\sin b}}{{\cos a\cos b - \sin a\sin b}}\)

                \[ = \frac{{\frac{{\sin a\cos b + \cos a\sin b}}{{\cos a\cos b}}}}{{\frac{{\cos a\cos b - \sin a\sin b}}{{\cos a\cos b}}}}\] (chia cả tử và mẫu cho cosacosb)

                \[ = \frac{{\frac{{\sin a\cos b}}{{\cos a\cos b}} + \frac{{\cos a\sin b}}{{\cos a\cos b}}}}{{\frac{{\cos a\cos b}}{{\cos a\cos b}} - \frac{{\sin a\sin b}}{{\cos a\cos b}}}}\]

                \[ = \frac{{\frac{{\sin a}}{{\cos a}} + \frac{{\sin b}}{{\cos b}}}}{{1 - \frac{{\sin a}}{{\cos a}}.\frac{{\sin b}}{{\cos b}}}}\]

                \[ = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\]

Vậy \[\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\].