Giải SGK Toán 11 CD Bài 2. Giới hạn của hàm số có đáp án

Lời giải

Sau bài học này chúng ta sẽ biết:

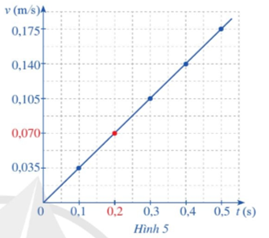
Trong toán học giá trị 0,070 được gọi là giới hạn của hàm số khi x tiến tới 0,2.

Lời giải

a) Ta có bảng giá trị sau:

Ta có: \[{\rm{limf}}({x_n}) = \lim \frac{{2\left( {n + 1} \right)}}{n} = 2\].

b) Lấy dãy (x_n) bất kí thỏa mãn x_n → 1 ta có:

f(x_n) = 2x_n

⇒ \[\lim f\left( {{x_n}} \right) = \lim 2{x_n} = 2\lim {x_n} = 2.1 = 2\].

Lời giải

Đặt f(x) = x²

Giả sử (x_n) là dãy số thỏa mãn limx_n = 2.

⇒ limf(x_n) = \(\lim x_n^2 = {2^2} = 4\).

Vậy \(\mathop {{\mathop{\rm l}\nolimits} i{\rm{m}}}\limits_{x \to 2} {{\rm{x}}^2} = 4\).

Lời giải

a) Giả sử (x_n) là dãy số bất kì thỏa mãn limx_n = 1. Khi đó ta có:

\(\lim f\left( {{x_n}} \right) = \lim \left( {x_n^2 - 1} \right) = \lim x_n^2 - 1 = 1 - 1 = 0\).

\( \Rightarrow \lim f\left( x \right) = 0\).

\(\lim g\left( {{x_n}} \right) = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = 2\)

\( \Rightarrow \lim g\left( x \right) = 2\).

b) Ta có: f(x) + g(x) = x² – 1 + x + 1 = x² + x

(x_n) là dãy số bất kì thỏa mãn limx_n = 1. Khi đó ta có:

\(\lim \left[ {f\left( {{x_n}} \right) + g\left( {{x_n}} \right)} \right] = \lim \left( {x_n^2 + {x_n}} \right) = \lim x_n^2 + \lim {x_n} = {1^2} + 1 = 2\).

\( \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = 2\).

Ta lại có: \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 + 2 = 2\).

Vậy \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) + g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) + \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 2\).

c) Ta có: f(x) – g(x) = x² – 1 – x – 1 = x² – x – 2

(x_n) là dãy số bất kì thỏa mãn limx_n = 1. Khi đó ta có:

\(\lim \left[ {f\left( {{x_n}} \right) - g\left( {{x_n}} \right)} \right] = \lim \left( {x_n^2 - {x_n} - 2} \right) = \lim x_n^2 - \lim {x_n} - 2 = {1^2} - 1 - 2 = - 2\).

\( \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = - 2\).

Ta lại có: \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0 - 2 = - 2\).

Vậy \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) - g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right) - \mathop {\lim }\limits_{x \to 1} g\left( x \right) = - 2\).

d) Ta có: f(x).g(x) = (x² – 1)(x + 1) = x³ + x² – x – 1

(x_n) là dãy số bất kì thỏa mãn limx_n = 1. Khi đó ta có:

\(\lim \left[ {f\left( {{x_n}} \right).g\left( {{x_n}} \right)} \right] = \lim \left( {x_n^3 + x_n^2 - {x_n} - 1} \right) = \lim x_n^3 + \lim x_n^2 - \lim {x_n} - 1 = {1^3} + {1^2} - 1 - 1 = 0\)

\( \Rightarrow \mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = 0\).

Ta lại có: \(\mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right) = 0.2 = 0\).

Vậy \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right).g\left( x \right)} \right] = \mathop {\lim }\limits_{x \to 1} f\left( x \right).\mathop {\lim }\limits_{x \to 1} g\left( x \right)\).

e) Ta có: \(\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^2} - 1}}{{x + 1}}\)

(x_n) là dãy số bất kì thỏa mãn limx_n = 1. Khi đó ta có:

\(\lim \frac{{f\left( {{x_n}} \right)}}{{g\left( {{x_n}} \right)}} = \lim \frac{{x_n^2 - 1}}{{{x_n} + 1}} = \lim \frac{{\left( {{x_n} - 1} \right)\left( {{x_n} + 1} \right)}}{{{x_n} + 1}} = \lim \left( {{x_n} - 1} \right) = 0\).

\( \Rightarrow \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = 0\).

Ta lại có: \(\frac{{\lim f\left( x \right)}}{{\lim g\left( x \right)}} = \frac{0}{2} = 0\)

Vậy \(\mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{\mathop {\lim }\limits_{x \to 1} f\left( x \right)}}{{\mathop {\lim }\limits_{x \to 1} g\left( x \right)}}\).

Lời giải

a) \(\mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 1} \right)\left( {{x^2} + 2x} \right)} \right] = \mathop {\lim }\limits_{x \to 2} \left( {x + 1} \right).\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + 2x} \right) = 3.8 = 24\).

b) \(\mathop {\lim }\limits_{x \to 2} \sqrt {{x^2} + x + 3} = \sqrt {\mathop {\lim }\limits_{x \to 2} \left( {{x^2} + x + 3} \right)} = 3\).

Lời giải

a) Xét dãy số (u_n) sao cho u_n < 0 và lim u_n = 0. Khi đó f(u_n) = – 1 và lim f(u_n) = – 1.

b) Xét dãy số (v_n) sao cho v_n > 0 và lim v_n = 0. Khi đó f(v_n) = 1 và lim f(v_n) = 1.