Phòng luyện đề thi giữa kì 1 năm học 2026-2027 tất cả các môn lớp 1-12

✕

Giảm 50% Kích hoạt VIP

Kích hoạt VIP

Tạo VIP

Giải SGK Toán 11 CD Bài 3. Hàm số liên tục có đáp án

33 người thi tuần này 4.6 726 lượt thi 15 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

35 người thi tuần này

Đề thi giữa kì 1 Toán 11 năm 2026-2027 THPT Việt Đức (Hà Nội) có đáp án

134 lượt thi 21 câu hỏi

24 người thi tuần này

Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Tạ Quang Bửu (Hà Nội) có đáp án

123 lượt thi 21 câu hỏi

40 người thi tuần này

Đề thi giữa kì 1 Toán 11 năm 2026-2027 THCS&THPT Nguyễn Bỉnh Khiêm (Hà Nội) có đáp án

139 lượt thi 22 câu hỏi

69 người thi tuần này

Trắc nghiệm Công thức nhân xác suất cho hai biến cố độc lập lớp 11 (có đúng sai, trả lời ngắn)

1.6 K lượt thi 20 câu hỏi

60 người thi tuần này

Trắc nghiệm Công thức cộng xác suất lớp 11 (có đúng sai, trả lời ngắn)

2.4 K lượt thi 20 câu hỏi

216 người thi tuần này

Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 2345

3 K lượt thi 21 câu hỏi

97 người thi tuần này

Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Phùng Khắc Khoan (Thạch Thất-Hà Nội) có đáp án - mã đề 0123

2.9 K lượt thi 21 câu hỏi

76 người thi tuần này

Đề thi cuối kì 1 Toán 11 năm 2025-2026 THPT Vạn Xuân (Hoài Đức-Hà Nội) có đáp án - Đề chẵn

2.8 K lượt thi 21 câu hỏi

Danh sách câu hỏi:

Câu 1/15

Cấu sông Hàn là một trong những cây cầu bắc qua sông Hàn ở Đà Nẵng. Đây là cây cầu đầu tiên do kĩ sư, công nhân Việt Nam tự thiết kế và thi công. Khi cầu không quay (Hình 10a), mặt cầu liền mạch nên các phương tiện có thể đi lại giữa hai đầu cầu. Khi cầu quay (Hình 10b) để các tàu, thuyền có thể đi qua thì mặt cầu không còn liền mạch nữa, các phương tiện không thể đi qua giữa hai đầu cầu.

Kiến thức gì trong toán học thể hiện chuyển động có đường đi là đường liền mạch?

Xem đáp án

Lời giải

Lời giải

Kiến thức trong toán học thể hiện chuyển động của đường đi là đường liên mạch đó là kiến thức về hàm số liên tục.

Để tìm hiểu kĩ hơn hàm số liên tục là gì thì chúng ta sẽ cùng tìm hiểu bài học ngày hôm nay. Bài học: “Hàm số liên tục”.

Câu 2/15

Quan sát đồ thị hàm số f(x) = x ở Hình 11.

a) Tính \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).

b) So sánh \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) và f(1).

Xem đáp án

Lời giải

Lời giải

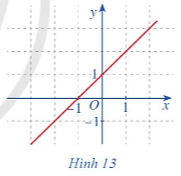
a) Ta có: \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} x = 1\).

b) Ta có: f(1) = 1 nên \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\).

Câu 3/15

Xét tính liên tục của hàm số f(x) = x³ + 1 tại x₀ = 1.

Xem đáp án

Lời giải

Lời giải

Ta có: \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^3} + 1} \right) = 2\) và f(1) = 1³ + 1 = 2

Suy ra \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right)\).

Vì vậy hàm số liên tục tại x₀ = 1.

Câu 4/15

Cho hàm số f(x) = x + 1 với x ∈ ℝ.

a) Giả sử x₀ ∈ ℝ. Hàm số f(x) có liên tục tại điểm x₀ hay không?

b) Quan sát đồ thị hàm số f(x) = x + 1 với x ∈ ℝ (Hình 13), nêu nhận xét về đặc điểm của đồ thị hàm số đó.

Xem đáp án

Lời giải

Lời giải

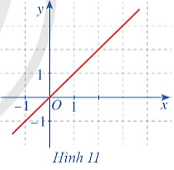
a) Với x₀ ∈ ℝ bất kì ta có: \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = {x_0} + 1 = f\left( {{x_0}} \right)\). Do đó hàm số liên tục tại x = x₀.

b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị x ∈ ℝ.

Câu 5/15

Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x - 1\,\,khi\,\,x < 2\\ - x\,\,\,\,\,\,khi\,\,x \ge 2\end{array} \right.\). Có liên tục trên ℝ hay không?

Xem đáp án

Lời giải

Lời giải

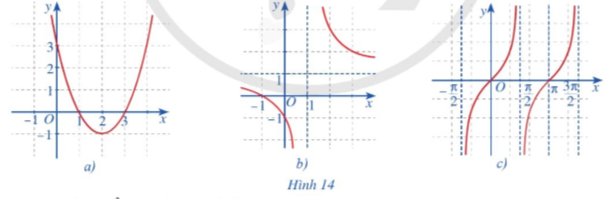
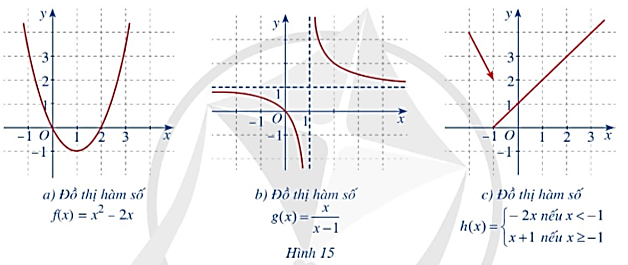
+) Với mỗi x₀ ∈ (– ∞; 2) có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x - 1} \right) = {x_0} - 1 = f\left( {{x_0}} \right)\) là hàm số liên tục.

+) Với mỗi x₀ ∈ (2; +∞) có \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( { - x} \right) = - {x_0} = f\left( {{x_0}} \right)\) là hàm số liên tục.

+) Tại x = 2, ta có: \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left( {x - 1} \right) = 1\) và f(2) = – 2 nên \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) \ne f\left( 2 \right)\).

Vậy hàm số không liên tục tại x = 2.

Câu 6/15

Quan sát đồ thị các hàm số: y = x² – 4x + 3 (Hình 14a); \(y = \frac{{x + 1}}{{x - 1}}\left( {x \ne 1} \right)\) (Hình 14b); y = tanx (Hình 14c) và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.

Xem đáp án

Lời giải

Lời giải

Hình 14a) đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ khoảng xác định.

Hình 14b) đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm đố liên tục trên từng khoảng xác định.

Hình 14c) đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

Câu 7/15

Hàm số \(f\left( x \right) = \frac{{x + 2}}{{x - 8}}\) có liên tục trên mỗi khoảng (– ∞; 8), (8; + ∞) hay không?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8/15

Cho hai hàm số f(x) = x³ + x và g(x) = x² + 1 (x ∈ ℝ). Hãy cho biết:

a) Hai hàm số f(x), g(x) có liên tục tại x = 2 hay không.

b) Các hàm số f(x) + g(x); f(x) – g(x); f(x).g(x); \(\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại x = 2 hay không.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9/15

Xét tính liên tục của hàm số f(x) = sinx + cosx trên ℝ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/15

Dùng định nghĩa xét tính liên tục của hàm số f(x) = 2x³ + x + 1 tại điểm x = 2.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/15

Trong các hàm số có đồ thị ở Hình 15a, 15b, 15c, hàm số nào liên tục trên tập xác định của hàm số đó? Giải thích.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/15

Bạn Nam cho rằng: “Nếu hàm số y = f(x) liên tục tại điểm x₀, còn hàm số y = g(x) không liên tục tại x₀, thì hàm số y = f(x) + g(x) không liên tục tại x₀”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/15

Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:

a) f(x) = x² + sinx;

b) g(x) = x⁴ – x² + \(\frac{6}{{x - 1}}\);

c) \(h\left( x \right) = \frac{{2x}}{{x - 3}} + \frac{{x - 1}}{{x + 4}}\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14/15

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + x + 1\,\,khi\,\,x \ne 4\\2a + 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 4.\end{array} \right.\)

a) Với a = 0, xét tính liên tục của hàm số tại x = 4.

b) Với giá trị nào của a thì hàm số liên tục tại x = 4?

c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15/15

Hình 16 biểu thị độ cao h(m) của một quả bóng đá lên theo thời gian t(s), trong đó h(t) = – 2t² + 8t.

a) Chứng tỏ hàm số h(t) liên tục trên tập xác định.

b) Dựa vào đồ thị hãy xác định \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right)\).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 9/15 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Khóa học 1 - 12

THPT

THCS

Phòng luyện đề

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ô Ôn vào 10

Ôn vào 6

Ô Ôn vào 6

Tài liệu

THPT

THCS

Tin Tuyển Sinh