Giải SGK Toán 11 Cánh Diều Phương trình lượng giác cơ bản có đáp án

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

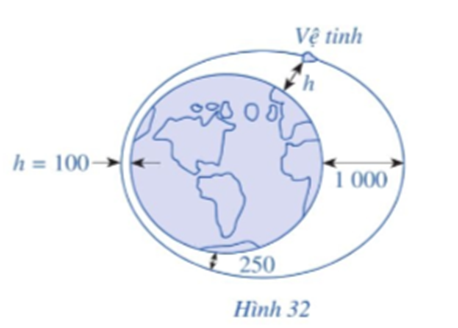
• Để vệ tinh cách mặt đất 1 000 km thì \(550 + 450\cos \frac{\pi }{{50}}t = 1\,\,\,000\)

\( \Leftrightarrow 450\cos \frac{\pi }{{50}}t = 450\)

\( \Leftrightarrow \cos \frac{\pi }{{50}}t = 1\)

\( \Leftrightarrow \frac{\pi }{{50}}t = k2\pi \,\,\,\left( {k \in \mathbb{Z},\,t \ge 0} \right)\)

\[ \Leftrightarrow t = k2\pi .\frac{{50}}{\pi } = 100k\,\,\left( {k \in \left\{ {0;1;2;3;...} \right\}} \right)\]

Vậy tại các thời điểm t = 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 1 000 km.

• Để vệ tinh cách mặt đất 250 km thì \(550 + 450\cos \frac{\pi }{{50}}t = 250\)

\( \Leftrightarrow 450\cos \frac{\pi }{{50}}t = - 300\)

\( \Leftrightarrow \cos \frac{\pi }{{50}}t = - \frac{2}{3}\)

\[ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{50}}t \approx 2,3 + k2\pi \\\frac{\pi }{{50}}t \approx - 2,3 + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}\,,\,\,t \ge 0} \right)\]

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp  ta được kết quả gần đúng là 2,3)

\[ \Leftrightarrow \left[ \begin{array}{l}t \approx \frac{{115}}{\pi } + 100k\\t \approx - \frac{{115}}{\pi } + 100k\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}\,,\,\,t \ge 0} \right)\]

Vậy tại các thời điểm \[t \approx \pm \frac{{115}}{\pi } + 100k\](với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 250 km.

• Để vệ tinh cách mặt đất 100 km thì \(550 + 450\cos \frac{\pi }{{50}}t = 1\,00\)

\( \Leftrightarrow 450\cos \frac{\pi }{{50}}t = - 450\)

\( \Leftrightarrow \cos \frac{\pi }{{50}}t = - 1\)

\( \Leftrightarrow \frac{\pi }{{50}}t = \pi + k2\pi \,\,\,\left( {k \in \mathbb{Z},\,t \ge 0} \right)\).

\( \Leftrightarrow t = 50 + 100k\,\,\,\left( {k \in \left\{ {0;1;2;3;...} \right\}} \right)\).

Vậy tại các thời điểm t = 50 + 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 100 km.

Ta có:

x² ‒ 3x + 2 = 0 (1)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (1) có tập nghiệm S₁ = {1; 2}.

(x – 1)(x – 2) = 0 (2)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (2) có tập nghiệm S₂ = {1; 2}.

Hai tập S₁, S₂ bằng nhau vì cùng là tập {1; 2}.

Tập nghiệm của phương trình x – 1 = 0 là S₁ = {1}.

Tập nghiệm của phương trình \(\frac{{{x^2} - 1}}{{x + 1}} = 0\) là S₂ = {1}.

Vì S₁ = S₂ nên hai phương trình x – 1 = 0 và \(\frac{{{x^2} - 1}}{{x + 1}} = 0\) tương đương.

Phương trình 3x ‒ 6 = 0 có tập nghiệm S₁ = {2}.

Phương trình 3x = 6 có tập nghiệm S₂ = {2}.

Vì S₁ = S₂ nên hai phương trình 3x ‒ 6 = 0 và 3x = 6 tương đương

Khi đó ta viết 3x ‒ 6 = 0 Û 3x = 6.

Vậy khẳng định 3x ‒ 6 = 0 Û 3x = 6 là khẳng định đúng.

Ta có: (x – 1)² = 5x – 11

       Û x² – 2x + 1 – (5x – 11) = 0

       Û x² – 2x + 1 – 5x + 11 = 0

       Û x² – 7x + 12 = 0

       Û x = 3 hoặc x = 4.

Vậy tập nghiệm của phương trình đã cho là S = {3; 4}.\(\)

Với x ∈ [‒π; π] ta thấy \(\sin x = \frac{1}{2}\) tại \(x = \frac{\pi }{6}\) và \(x = \frac{{5\pi }}{6}\).

Do đó đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A₀, B_0­ có hoành độ lần lượt là \({x_{{A_0}}} = \frac{\pi }{6}\) và \({x_{{B_0}}} = \frac{{5\pi }}{6}\).

Với x ∈ [π; 3π] ta thấy \(\sin x = \frac{1}{2}\) tại \(x = \frac{{13\pi }}{6}\) và \(x = \frac{{17\pi }}{6}\).

Do đó đường thẳng \(d:y = \frac{1}{2}\) cắt đồ thị hàm số y = sinx, x ∈ [π; 3π] tại hai giao điểm A₁, B_1­ có hoành độ lần lượt là \({x_{{A_1}}} = \frac{{13\pi }}{6}\) và \({x_{{B_1}}} = \frac{{17\pi }}{6}\).