Giải SGK Toán 11 CD Bài 1. Giới hạn của dãy số có đáp án
37 người thi tuần này 4.6 731 lượt thi 20 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 7 (có lời giải) - Đề 1
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 3
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 2
Đề kiểm tra Các quy tắc tính đạo hàm (có lời giải) - Đề 1
Đề kiểm tra Bài tập cuối chương 6 (có lời giải) - Đề 3
Danh sách câu hỏi:
Lời giải
Lời giải
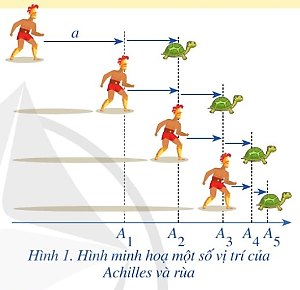
Giới hạn hữu hạn của hàm số có thể giải thích được nghịch lí Zénon nói trên là không đúng. Trong bài học ngày hôm nay chúng ta sẽ tìm hiểu về điều đó.Lời giải
Lời giải
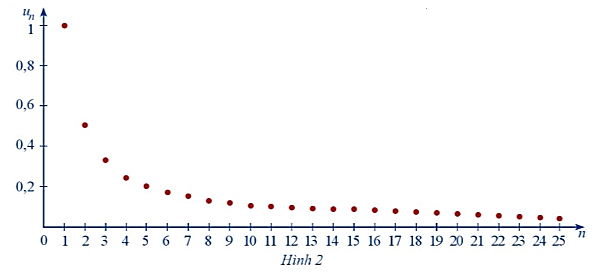
a) Khi n ngày càng lớn thì giá trị của un càng giảm dần về 0.
b) Ta có bảng:
|
n |
1 000 |
1 001 |
... |
10 000 |
10 001 |
... |
|
|un – 0| |
0,001 |
0,00099... |
... |
0,0001 |
0,000099... |
... |
Kể từ số hạng u1001 trở đi thì khoảng cách từ un đến 0 nhỏ hơn 0,001.
Kể từ số hạng u10 001 trở đi thì khoảng cách từ un đến 0 nhỏ hơn 0,0001.
Lời giải
Lời giải
a) Ta có: un = 0 với mọi n ∈ ℕ*
Với mọi ε > 0 bé tùy ý, ta có:
|un – 0| < ε với mọi n ∈ ℕ*
Vậy lim 0 = 0.
b) Ta có: un = \(\frac{1}{{\sqrt n }}\) với mọi n ∈ ℕ*
Với mọi ε > 0 bé tùy ý, ta có:
|un – 0| < ε ⇔ \(\left| {\frac{1}{{\sqrt n }}} \right| < \varepsilon \Leftrightarrow \sqrt n > \frac{1}{\varepsilon } \Leftrightarrow n > \frac{1}{{{\varepsilon ^2}}}\).
Chọn N ≥ \(\frac{1}{{{\varepsilon ^2}}}\) thì với mọi n >N ta có: \(\left| {\frac{1}{{\sqrt n }}} \right| < \varepsilon \)
Vì vậy \(\lim \frac{1}{{\sqrt n }} = 0\).Lời giải
Lời giải
Ta có: un – 2 = 2 + \(\frac{1}{n}\) – 2 = \(\frac{1}{n}\)
Với mọi ε > 0 bé tùy ý, ta có:
|un – 0| < ε ⇔ \(\left| {\frac{1}{n}} \right| < \varepsilon \Leftrightarrow n > \frac{1}{\varepsilon }\).
Chọn N ≥ \(\frac{1}{\varepsilon }\) thì với mọi n > N ta có: \(\left| {\frac{1}{n}} \right| < \varepsilon \)
Vì vậy \(\lim \left( {{u_n} - 2} \right) = 0\).
Lời giải
Lời giải
Đặt un =\(\frac{{ - 4n + 1}}{n}\), suy ra un – 4 = \(\frac{{ - 4n + 1}}{n} - \left( { - 4} \right) = \frac{1}{n}\)
Do đó \(\lim \left( {{u_n} - \left( { - 4} \right)} \right) = \lim \frac{1}{n} = 0\).
\( \Rightarrow \lim {u_n} = - 4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.