Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.34. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.
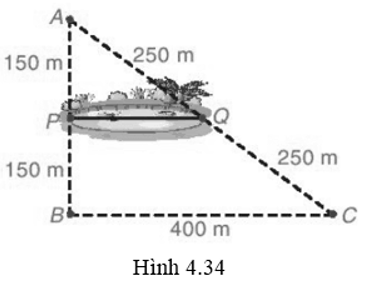
Bác Mến muốn tính khoảng cách giữa hai vị trí P, Q ở hai bên bờ ao cá. Để làm điều đó, bác Mến chọn ba vị trí A, B, C, thực hiện đo đạc và vẽ mô phỏng như Hình 4.34. Em hãy giúp bác Mến tính khoảng cách giữa hai điểm P và Q.

Câu hỏi trong đề: Giải VTH Toán 8 KNTT Bài tập cuối chương 4 đáp án !!
Quảng cáo
Trả lời:
∆ABC có: P là trung điểm AB, Q là trung điểm AC nên PQ là đường trung bình của ∆ABC. Suy ra PQ // BC và PQ = BC = 200 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
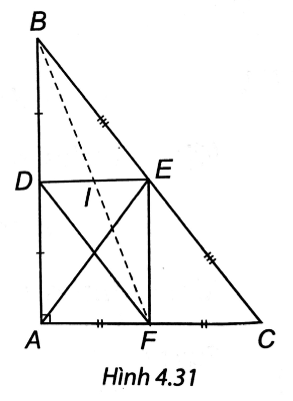
a) ∆ABC có: D là trung điểm AB, E là trung điểm BC, nên DE là đường trung bình của ∆ABC.
Suy ra DE // AC và DE = AC.
Xét tứ giác ADEF: DE // AF và DE = AF nên tứ giác ADEF là hình bình hành.
Ta lại có nên tứ giác ADEF là hình chữ nhật.
Suy ra AE = DF.
b) ∆ABC có: D là trung điểm AB, F là trung điểm AC nên DF là đường trung bình của ∆ABC.
Suy ra DF // BC và DF = BC = BE.
Xét tứ giác BDFE: DF // BE và DF = BE nên tứ giác BDFE là hình bình hành.
Suy ra hai đường chéo DE và BF cắt nhau tại trung điểm của mỗi đường.
Ta lại có I là trung điểm của DE nên I cũng là trung điểm của BF.
Vậy B, I, F thẳng hàng.
Lời giải
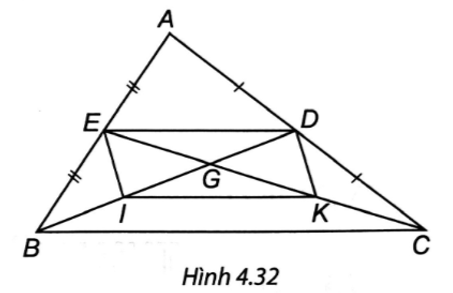
∆ABC có: E là trung điểm AB, D là trung điểm AC nên ED là đường trung bình của ∆ABC. Suy ra ED // BC và ED = BC. (1)
∆GBC có: I là trung điểm GC, K là trung điểm GB nên IK là đường trung bình của ∆GBC. Suy ra IK // BC và IK = BC. (2)
Từ (1) và (2) suy ra ED // IK và ED = IK nên tứ giác EDKI là hình bình hành.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.