Câu hỏi:

13/07/2024 244

Trong không gian Oxyz, cho hai điểm $A (2; - 2; 4), B (- 3; 3; - 1)$ và mặt phẳng $(P) : 2 x - y + 2 z - 8 = 0$ . Xét M là điểm thay đổi thuộc (P), giá trị nhỏ nhất của $2 M A^{2} + 3 M B^{2}$ bằng bao nhiêu?

Xem lời giải

Câu hỏi trong đề: Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 11) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi I là điểm thỏa mãn $2 \vec{I A} + 3 \vec{I B} = \vec{0}$ , suy ra $I (- 1; 1; 1)$ .

Khi đó ta có:

$2 M A^{2} + 3 M B^{2} = 2 {(\vec{M I} + \vec{I A})}^{2} + 3 {(\vec{M I} + \vec{I B})}^{2} = 5 M I^{2} + 2 I A^{2} + 3 I B^{2}$

Do I, A, B cố định nên $2 M A^{2} + 3 M B^{2}$ nhỏ nhất khi MI nhỏ nhất, mà điểm M di động trên mặt phẳng (P) nên MI nhỏ nhất khi M là hình chiếu của điểm I trên mặt phẳng (P). Khi đó ta có $\min M I = d (I, (P)) = 3$ . Do đó $\min (2 M A^{2} + 3 M B^{2}) = 5.9 + 2.27 + 3.12 = 135$ .

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(1;-1) và bán kính R = 5. Biết rằng đường thẳng (d): 3x -4y +8 = 0 cắt đường tròn (C) tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB.

A. AB = 4

B. AB = 3

C. AB = 8

D. AB = 6

Lời giải

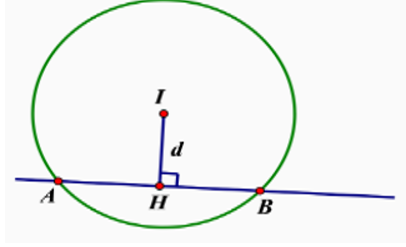
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(1;-1) và bán kính R = 5. Biết rằng đường thẳng (d): 3x -4y +8 = 0 cắt đường tròn (C) tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB. (ảnh 1)

Khoảng cách từ tâm / đến đường thẳng d bằng $d (I, d) = \frac{| 3 + 4 + 8 |}{5} = 3$ .

Áp dụng công thức $R^{2} = d^{2} (I, d) + \frac{A B^{2}}{4}$ ta có

$5^{2} = 3^{2} + \frac{A B^{2}}{4} \Rightarrow \frac{A B^{2}}{4} = 4^{2} \Rightarrow A B = 8$

Câu 2

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G1,G2 lần lượt là trọng tâm của $Δ A B C$ và $Δ S B C$ . Khi đó

A. $G_{1} G_{2} / / (S A B)$

B. $G_{1} G_{2} / / (S B D)$ .

G_{1} G_{2} / / (S C D)

G_{1} G_{2} / / (S B C)

Lời giải

Gọi I là trung điểm cạnh đáy BC. Xét $Δ S A I$ , ta có: $\frac{I G_{1}}{I A} = \frac{I G_{2}}{I S} = \frac{1}{3}$ $\Rightarrow G_{1} G_{2} / / S A$

Do đó: $\{\begin{array}{l} G_{1} G_{2} \subset (S A B) \\ G_{1} G_{2} / / S A \\ S A \subset (S A B) \end{array} \Rightarrow G_{1} G_{2} / / (S A B)$

Câu 3

Hàm số nào có đồ thị như hình vẽ ỏ bên đây ?

y = {(\frac{1}{3})}^{x}

y = 3^{x}

y = {(\sqrt{2})}^{x}

y = {(\frac{1}{\sqrt{2}})}^{2}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Khí hậu Đông Nam Á biển đảo chủ yếu là

A. cận xích đạo và cận nhiệt đới.

B. nhiệt đới gió mùa và khí hậu xích đạo.

C. nhiệt đới gió mùa và ôn đới gió mùa.

D. nhiệt đới gió mùa và cận nhiệt đới.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho phản ứng hạt nhân : $T + X \to α + n$ . X là hạt nhân.

A. Đoteri

B. Triti

C. notron

D. proton

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hình trụ có chiều cao bằng 6a. Biết rằng khi cắt hình trụ đã cho bời một mặt phẳng song song với trục và cách trục một khoàng bằng 3a, thiết diện thu được là một hình vuông. Thể tích của khối trục được giới hạn bời hình trụ đã cho bằng $m π a^{3}$ . Tính m.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Nội dung nào trong trong Hiệp định Pari năm 1973 về Việt Nam đã khắc phục được một trong những hạn chế của Hiệp định Giơnevơ năm 1954 về Đông Dương?

A. Các nước tham dự Hội nghị cam kết tôn trọng các quyền dân tộc cơ bản của nhân dân Việt Nam.

B. Hoa Kì và đồng minh rút hết quân đội khỏi miền Nam, quân đội miền Bắc không phải tập kết ra Bắc.

C. Hai bên trao trả tù binh và dân thường bị bắt.

D. Các bên thực hiện ngừng bắn, lập lại hòa bình ở Việt Nam.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Trong không gian Oxyz, cho hai điểm A(2;−2;4),B(−3;3;−1) và mặt phẳng (P):2x−y+2z−8=0. Xét M là điểm thay đổi thuộc (P), giá trị nhỏ nhất của 2MA2+3MB2 bằng bao nhiêu?

Bình luận

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(1;-1) và bán kính R = 5. Biết rằng đường thẳng (d): 3x -4y +8 = 0 cắt đường tròn (C) tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G1,G2 lần lượt là trọng tâm của ΔABC và ΔSBC. Khi đó

Hàm số nào có đồ thị như hình vẽ ỏ bên đây ?

Khí hậu Đông Nam Á biển đảo chủ yếu là

Cho phản ứng hạt nhân : T+X→α+n. X là hạt nhân.

Nội dung nào trong trong Hiệp định Pari năm 1973 về Việt Nam đã khắc phục được một trong những hạn chế của Hiệp định Giơnevơ năm 1954 về Đông Dương?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong không gian Oxyz, cho hai điểm $A (2; - 2; 4), B (- 3; 3; - 1)$ và mặt phẳng $(P) : 2 x - y + 2 z - 8 = 0$ . Xét M là điểm thay đổi thuộc (P), giá trị nhỏ nhất của $2 M A^{2} + 3 M B^{2}$ bằng bao nhiêu?

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G1,G2 lần lượt là trọng tâm của $Δ A B C$ và $Δ S B C$ . Khi đó

Cho phản ứng hạt nhân : $T + X \to α + n$ . X là hạt nhân.