Cho hình vẽ, có \(\widehat {BAC}\) = 50°, \(\widehat {ABC}\) = 65°, Ax // BC.
a) Tính số đo \(\widehat {ACB}\).
b) Tính số đo \(\widehat {yAx}\) rồi chứng minh Ax là tia phân giác của \(\widehat {yAC}\).
c) Vẽ tia Az là tia đối của tia Ax, tia Am là tia phân giác của zAB, tia Bn là tia phân giác của \(\widehat {ABC}\). Chứng minh Am // Bn.
Cho hình vẽ, có \(\widehat {BAC}\) = 50°, \(\widehat {ABC}\) = 65°, Ax // BC.
a) Tính số đo \(\widehat {ACB}\).
b) Tính số đo \(\widehat {yAx}\) rồi chứng minh Ax là tia phân giác của \(\widehat {yAC}\).
c) Vẽ tia Az là tia đối của tia Ax, tia Am là tia phân giác của zAB, tia Bn là tia phân giác của \(\widehat {ABC}\). Chứng minh Am // Bn.
Quảng cáo
Trả lời:
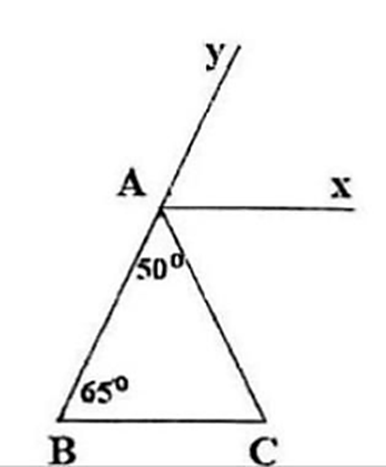
a) Xét tam giác ABC có:
\(\widehat {BAC} + \widehat {ABC} + \widehat {ACB}\) = 180°
⇔ 50° + 65° + \(\widehat {ACB}\)= 180°
⇔ \(\widehat {ACB}\)= 65°
b) Do Ax // BC nên \(\widehat {ACB} = \widehat {CAx} = 65^\circ \)(so le trong)
Suy ra: \(\widehat {BAx} = 50^\circ + 65^\circ = 115^\circ \)
Ta có: \(\widehat {BAx} + \widehat {yAx} = 180^\circ \)
⇔ \(\widehat {yAx} = 180^\circ - 115^\circ = 65^\circ \)
Suy ra: \(\widehat {yAx} = \widehat {CAx} = 65^\circ \)nên Ax là tia phân giác \(\widehat {yAC}\)
c) Do Az là tia đối của Ax nên \(\widehat {xAz} = 180^\circ \)
Lại có: \(\widehat {xAz} = \widehat {BAx} + \widehat {BAz}\)
Suy ra: \(\widehat {BAz} = 180^\circ - 115^\circ = 65^\circ \)
Do Am là phân giác của \(\widehat {BAz}\)
nên \[\widehat {BAm} = \frac{1}{2}\widehat {BAz} = \frac{1}{2}.65^\circ = 32,5^\circ \]
Mặt khác: Bn là phân giác của \(\widehat {ABC}\)
nên \[\widehat {ABn} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}.65^\circ = 32,5^\circ \]
Do đó: \[\widehat {BAm} = \widehat {ABn}\]mà 2 góc này ở vị trí so le trong
Nên Am // Bn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
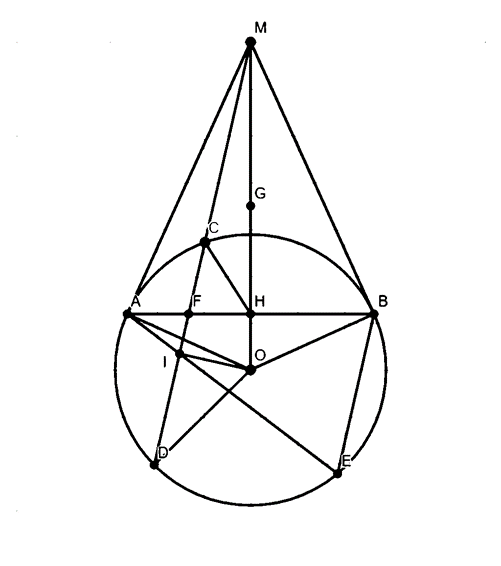
a) Vì MA, MB là tiếp tuyến của (O)
⇒ \(\widehat {MAO} = \widehat {MBO} = 90^\circ \)
Tứ giác AOBM có \(\widehat {MAO} + \widehat {MBO} = 90^\circ + 90^\circ = 180^\circ \)
⇒ A, O, B, M thuộc đường tròn đường kính OM.
⇒ AOBM nội tiếp đường tròn đường kính OM.
Tâm G là trung điểm OM
b. Vì MA là tiếp tuyến của (O)
⇒ \(\widehat {MAC} = \widehat {MDA}\) (góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung AC)
Lại có \(\widehat M\)chung.
Do đó, ΔMAC ∽ ΔMDA(g.g)
⇒ \(\frac{{MA}}{{MD}} = \frac{{MC}}{{MA}}\)
⇒ MA2 = MC.MD.
c) Vì I là trung điểm CD ⇒ OI ⊥ CD
⇒ OI ⊥ MI
⇒ I thuộc đường tròn đường kính OM
⇒ I ∈ (G)
⇒ M, A, O, I, B ∈ (G).
d) Vì MA, MB là tiếp tuyến của (O)
Nên MA = MB, MO là phân giác \[\widehat {AMB}\]
⇒ ΔMAB có MO vừa là phân giác vừa là đường cao.
⇒ MO ⊥ AB
Áp dụng hệ thức lượng vào ΔAMO đường cao AH có:
⇒ MA2 = MH.MO (kết hợp b)
⇒ MH.MO = MC.MD
⇒ \(\frac{{MC}}{{MO}} = \frac{{MH}}{{MD}}\)
Xét ΔMCH và ΔMOD có:
\(\frac{{MC}}{{MO}} = \frac{{MH}}{{MD}}\)
\(\widehat M\)chung
Do đó, ΔMCH ∽ ΔMOD (c.g.c).
⇒ \(\widehat {MHC} = \widehat {MDO} = \widehat {CDO}\)
⇒ CHOD nội tiếp
e) Gọi CD ∩ AB = F
⇒ \(\widehat {AFI} = \widehat {ABE}\) (vì CD // BE và hai góc ở vị trí đồng vị)
Ta có: A, M, B, O, I ∈ (G)
⇒ \(\widehat {AIC} = \widehat {AIM} = \widehat {AOM} = \frac{1}{2}\widehat {AOB} = \widehat {AEB}\)
⇒ \(\widehat {AIF} = \widehat {AEB}\)
⇒ ΔAIF ∽ ΔAEB (g.g).
⇒ \(\widehat {IAF} = \widehat {EAB} = \widehat {EAF}\)
⇒ A, I, E thẳng hàng.
Lời giải
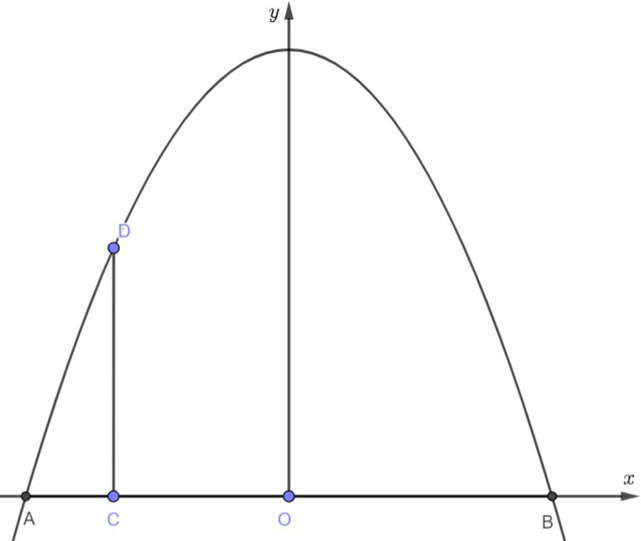
AB = 9m
AC = 0,5m
CD = 1,6m
Gọi O là trung điểm của A
Dựng hệ Oxy thỏa mãn A,B thuộc Ox và Oy ⊥ AB tại O
OB = \(\frac{9}{2}\), OC = \(\frac{9}{2} - 0,5 = 4\)
Cổng là (P) có phương trình dạng y = ax2 + b
Có: \(\left\{ \begin{array}{l}B = \left( {\frac{9}{2};0} \right) \in \left( P \right)\\D = \left( { - 4;1,6} \right) \in \left( P \right)\end{array} \right.\)
⇔ \(\left\{ \begin{array}{l}0 = a.{\left( {\frac{9}{2}} \right)^2} + b\\1,6 = a.{\left( { - 4} \right)^2} + b\end{array} \right.\)
⇔\(\left\{ \begin{array}{l}a = \frac{{ - 32}}{{85}}\\b = \frac{{648}}{{85}}\end{array} \right.\)
Tung độ ứng với hoành độ bằng 0 là y = a.02 + b = \(\frac{{648}}{{85}}\)
Vậy chiều cao của cổng Parabol là \(\frac{{648}}{{85}} \approx 7,6m.\)
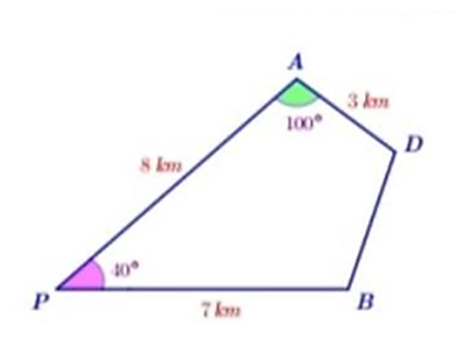
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.