Câu hỏi:

12/07/2024 4,205

Cho hình vuông ABCD, M là một điểm nằm giữa B và C. Kẻ AN vuông góc với AM, AP vuông góc với MN (N và P thuộc đường thẳng CD).

a) Chứng minh tam giác AMN vuông cân và AN² = NC . NP

b) Tính tỉ số chu vi tam giác CMP và chu vi hình vuông ABCD.

c) Gọi Q là giao điểm của tia AM và tia DC. Chứng minh tổng \(\frac{1}{{A{M^2}}} + \frac{1}{{A{Q^2}}}\) không đổi khi điểm M thay đổi trên cạnh BC.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

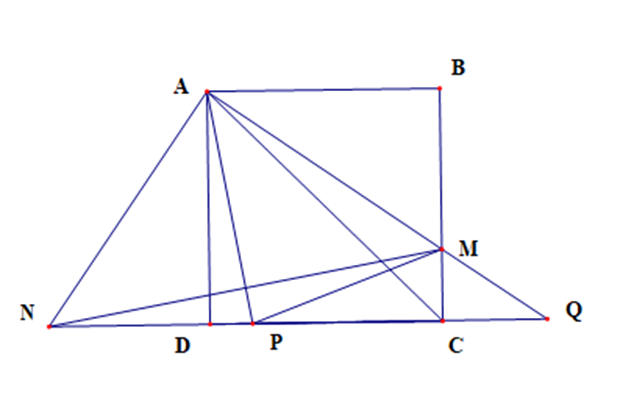
Cho hình vuông ABCD, M là một điểm nằm giữa B và C. Kẻ AN vuông góc với AM (ảnh 1)

a) Vì ABCD là hình vuông nên AB = BC = CD = DA và \(\widehat {ABC} = \widehat {BC{\rm{D}}} = \widehat {C{\rm{D}}A} = \widehat {DAB} = 90^\circ \)

Ta có:

\(\widehat {MAN} = \widehat {MA{\rm{D}}} + \widehat {DAN} = 90^\circ \)

\(\widehat {BA{\rm{D}}} = \widehat {MA{\rm{D}}} + \widehat {MAB} = 90^\circ \)

Suy ra \(\widehat {DAN} = \widehat {BAM}\)

Xét tam giác ADN và tam giác ABM có

\(\widehat {A{\rm{D}}N} = \widehat {ABM}\left( { = 90^\circ } \right)\)

AD = AB (chứng minh trên)

\(\widehat {DAN} = \widehat {BAM}\) (chứng minh trên)

Suy ra ∆ADN = ∆ABM (g.c.g)

Do đó AM = AN, DN = BM (các cặp cạnh tương ứng)

Suy ra tam giác AMN cân tại A

Khi đó tam giác AMN vuông cân tại A

Xét tam giác AMN cân tại A có AP là đường cao nên AP đồng thời là phân giác

Do đó \(\widehat {NAP} = \widehat {MAP} = \frac{1}{2}\widehat {MAN} = \frac{1}{2}.90^\circ = 45^\circ \)

Vì ABCD là hình vuông có CA là đường chéo nên \(\widehat {AC{\rm{D}}} = \widehat {ACB} = \frac{{90^\circ }}{2} = 45^\circ \)

Xét ∆ACN và ∆PAN có

\(\widehat {NAP} = \widehat {NCA}\left( { = 45^\circ } \right)\)

\(\widehat {ANC}\) là góc chung

Suy ra (g.g)

Do đó \(\frac{{AN}}{{PN}} = \frac{{CN}}{{AN}}\)

Hay AN² = NC . NP

b) Xét tam giác APN và tam giác APM có

AP là cạnh chung

\(\widehat {PAN} = \widehat {PAM}\) (chứng minh câu a)

AN = AM (chứng minh câu a)

Suy ra ∆APN = ∆APM (c.g.c)

Do đó PM = PN (hai cạnh tương ứng)

Chu vi tam giác MCP là:

CM + MP + CP = CM + PN + CP = CM + PB + DN + CP

= CM + PB + BM + CP = (CM + BM) + (PB + CP) = CD + CB = 2BC

Chu vi hình vuông ABCD là: 4BC

Vậy tỉ số chu vi tam giác CMP và chu vi hình vuông ABCD bằng \(\frac{{2BC}}{{4BC}} = \frac{1}{2}\)

c) Ta có: \[{{\rm{S}}_{ANQ}} = \frac{1}{2}AN.AQ = \frac{1}{2}A{\rm{D}}.NQ\]

Suy ra \(\frac{1}{{A{\rm{D}}}} = \frac{{NQ}}{{AN.AQ}}\)

Do đó \(\frac{1}{{A{{\rm{D}}^2}}} = \frac{{N{Q^2}}}{{A{N^2}.A{Q^2}}}\)

Vì tam giác ANQ vuông tại A nên AN² + AQ² = NQ²

Suy ra \(\frac{1}{{A{{\rm{D}}^2}}} = \frac{{A{N^2} + A{Q^2}}}{{A{N^2}.A{Q^2}}} = \frac{1}{{A{N^2}}} + \frac{1}{{A{Q^2}}}\)

Vì AD là cạnh hình vuông nên AD không đổi

Suy ra tổng \(\frac{1}{{A{M^2}}} + \frac{1}{{A{Q^2}}}\) không đổi khi điểm M thay đổi trên cạnh BC

Vậy tổng \(\frac{1}{{A{M^2}}} + \frac{1}{{A{Q^2}}}\) không đổi khi điểm M thay đổi trên cạnh BC.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hãy chứng minh 1 + 1 = 3.

Xem đáp án

Lời giải

Ta có:

1 + 1 = 3 ⟺ 2 = 3

Giả sử ta có đẳng thức:

14 + 6 – 20 = 21 + 9 – 30

Đặt thừa số chung ta có

2 × (7 + 3 – 10) = 3 × (7 + 3 – 10)

Theo toán học thì hai tích bằng nhau và có thừa số thứ hai bằng nhau thì thừa số thứ nhất bằng nhau

Do đó 2 = 3

Phản biện:

+) Sự thật 2 không thể bằng 3. Bài toán này sai trong lí luận của chúng ta là ở chỗ ta kết luận rằng: Hai tích bằng nhau và có thừa số thứ hai bằng nhau thì thừa số thứ nhất cũng bằng nhau. Điều đó không phải bao giờ cũng đúng.

+) Kết luận đó đúng khi và chỉ khi hai thừa số bằng nhau đó khác 0. Khi đó ta có thể chia 2 vế của đẳng thức cho số đó. Trong trường hợp thừa số đó bằng 0, thì luôn luôn có a × 0 = b × 0 với bất kì giá trị nào của a và b.

Ta có: 1 + 1 = 2 + 1

Mà (1 + 1) × 0 = (2 + 1 ) × 0

Vậy 1 + 1 = 3.

Câu 2