Quãng đường AB gồm một đoạn lên dốc dài 4 km và một đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
Quãng đường AB gồm một đoạn lên dốc dài 4 km và một đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4 km và đoạn xuống dốc dài 5 km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là \(\frac{4}{x}\) (h), thời gian xuống dốc là: \(\frac{5}{y}\) (h)
Theo đầu bài thời gian đi A đến B là 40 phút \( = \frac{2}{3}\) (h) nên:
\(\frac{4}{x} + \frac{5}{y} = \frac{2}{3}\) (1)
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là \(\frac{5}{x}\) (h), thời gian xuống dốc là: \(\frac{4}{y}\) (h)
Theo đầu bài thời gian đi A đến B là 41 phút \( = \frac{{41}}{{60}}\) (h) nên:
\(\frac{5}{x} + \frac{4}{y} = \frac{{41}}{{60}}\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}\frac{4}{x} + \frac{5}{y} = \frac{2}{3}\\\frac{5}{x} + \frac{4}{y} = \frac{{41}}{{60}}\end{array} \right.\)
Đăth \(X = \frac{1}{x};Y = \frac{1}{y}\) khi đó hệ phương trình trên trở thành:
\(\left\{ \begin{array}{l}4X + 5Y = \frac{2}{3}\\5X + 4Y = \frac{{41}}{{60}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}X = \frac{1}{{12}}\\Y = \frac{1}{{15}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 12\\y = 15\end{array} \right.\) (TMĐK)
Vậy tốc độ lúc lên dốc là 12 km/h, vận tốc lúc xuông dốc là 15 km/h.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{{a\sqrt 3 }}{4}\);
B. \(\frac{{a\sqrt 2 }}{4}\);
C. \(\frac{{a\sqrt 5 }}{4}\);
D. \(\frac{{a\sqrt 3 }}{3}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
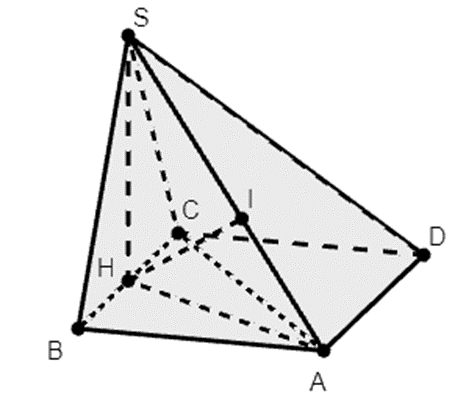
Gọi H là trung điểm của BC. Khi đó SH ⊥ (ABCD).
Do tam giác ABC vuông cân tại A nên AH ⊥ BC và \(AH = \frac{a}{2}\).
Dựng điểm D sao cho ABCD là hình bình hành.
Khi đó d(SA, BC) = d(BC, (SAD)) = d(H, (SAD)).
Kẻ HI ⊥ SA.
Khi đó d(H, (SAD)) = HI \( = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{a}{2}}}{a} = \frac{{a\sqrt 3 }}{4}\).
Câu 2
A. −259;
B. 68;
C. 0;
D. −4.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
TXĐ: D = ℝ
Hàm số liên tục trên đoạn [0; 4]
Ta có: y¢ = 3x2 + 4x – 7 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 1 \in [0;4]\\x = - \frac{7}{3} \notin [0;4]\end{array} \right.\)
Khi đó y(0) = 0; y(1) = −4; y(4) = 68
Vậy giá trị nhỏ nhất cần tìm là: −4.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left[ \begin{array}{l}x = 3\\x = - {\log _5}2\end{array} \right.\);
B. \(\left[ \begin{array}{l}x = 3\\x = {\log _5}2\end{array} \right.\);
C. \(\left[ \begin{array}{l}x = 1\\x = - {\log _5}2\end{array} \right.\);
D. \(\left[ \begin{array}{l}x = 1\\x = {\log _5}2\end{array} \right.\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{{a\sqrt {15} }}{5}\);
B. \(\frac{{2a\sqrt {15} }}{5}\);
C. \(\frac{{4a\sqrt {15} }}{5}\);
D. \(\frac{{5a\sqrt {15} }}{5}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[{\log _5}\left( {\frac{{1 - \sqrt {21} }}{2}} \right)\];
B. \({\log _5}\left( {\frac{{1 + \sqrt {21} }}{2}} \right)\);
C. 5;
D. \(5\log \left( {\frac{{1 + \sqrt {21} }}{2}} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập