Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Độ dài đường chéo AC’ là:
A. \(AC' = \sqrt {{a^2} + {b^2} + {c^2}} \);
B. \(AC' = \sqrt { - {a^2} + {b^2} + {c^2}} \);
C. \(AC' = \sqrt {{a^2} + {b^2} - {c^2}} \);
D. \(AC' = \sqrt {{a^2} - {b^2} + {c^2}} \).
Quảng cáo
Trả lời:
Đáp án đúng là: A
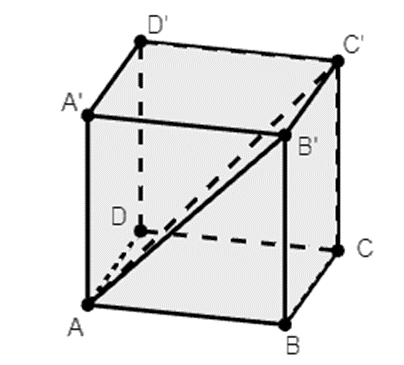
Ta có: C’B ⊥ (ABB’A’) nên suy ra ∆AB’C’ vuông tại B’.
(AB’)2 = a2 + c2
Khi đó ta có: \(AC' = \sqrt {{{(AB')}^2} + {{(B'C')}^2}} \)
\( = \sqrt {{a^2} + {c^2} + {b^2}} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{{a\sqrt 3 }}{4}\);
B. \(\frac{{a\sqrt 2 }}{4}\);
C. \(\frac{{a\sqrt 5 }}{4}\);
D. \(\frac{{a\sqrt 3 }}{3}\).
Lời giải
Đáp án đúng là: A
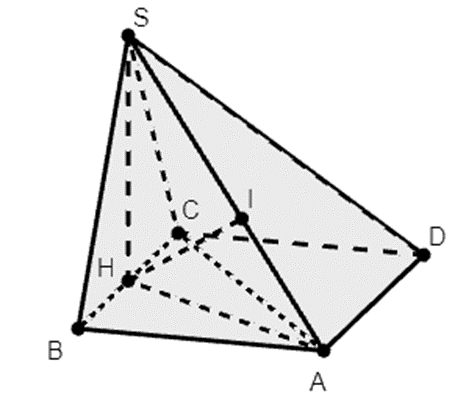
Gọi H là trung điểm của BC. Khi đó SH ⊥ (ABCD).
Do tam giác ABC vuông cân tại A nên AH ⊥ BC và \(AH = \frac{a}{2}\).
Dựng điểm D sao cho ABCD là hình bình hành.
Khi đó d(SA, BC) = d(BC, (SAD)) = d(H, (SAD)).
Kẻ HI ⊥ SA.
Khi đó d(H, (SAD)) = HI \( = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{a}{2}}}{a} = \frac{{a\sqrt 3 }}{4}\).
Câu 2
A. −259;
B. 68;
C. 0;
D. −4.
Lời giải
Đáp án đúng là: D
TXĐ: D = ℝ
Hàm số liên tục trên đoạn [0; 4]
Ta có: y¢ = 3x2 + 4x – 7 = 0
\( \Leftrightarrow \left[ \begin{array}{l}x = 1 \in [0;4]\\x = - \frac{7}{3} \notin [0;4]\end{array} \right.\)
Khi đó y(0) = 0; y(1) = −4; y(4) = 68
Vậy giá trị nhỏ nhất cần tìm là: −4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[{\log _5}\left( {\frac{{1 - \sqrt {21} }}{2}} \right)\];
B. \({\log _5}\left( {\frac{{1 + \sqrt {21} }}{2}} \right)\);
C. 5;
D. \(5\log \left( {\frac{{1 + \sqrt {21} }}{2}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\left[ \begin{array}{l}x = 3\\x = - {\log _5}2\end{array} \right.\);
B. \(\left[ \begin{array}{l}x = 3\\x = {\log _5}2\end{array} \right.\);
C. \(\left[ \begin{array}{l}x = 1\\x = - {\log _5}2\end{array} \right.\);
D. \(\left[ \begin{array}{l}x = 1\\x = {\log _5}2\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.