Câu hỏi:

18/08/2023 1,503

Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG.

a) Chứng minh tứ giác BCGE là hình thang cân.

b) Gọi K là giao điểm của các tia DE và FG, M là trung điểm của đoạn thẳng EG. Chứng minh ba điểm K, A, M thẳng hàng.

c) Chứng minh \(\widehat {COD} = 90^\circ \).

d) Chứng minh DC, FB và AM đồng quy.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

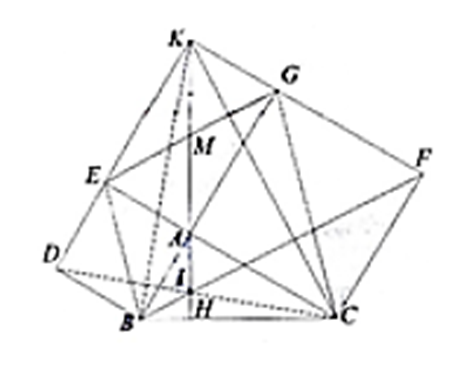
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE (ảnh 1)

a) Vì ABDE, ACFG là các hình vuông nên ta có E, A, C thẳng hàng và B, A, G cũng thẳng hàng (1) và EC = BG.

Mà \(\widehat {EBA} = \widehat {AGC} = 45^\circ \)(2).

Từ (1) và (2):

Suy ra EB // CG và EC = BG nên EBCG là hình thang cân.

b) Ta có: \(\widehat {AEK} = \widehat {GAE} = \widehat {AGK} = 90^\circ \)

Suy ra: AEKG là hình chữ nhật, hai đường chéo EG và AK giao nhau tại trung điểm mỗi đường.

Mà M là trung điểm EG

Nên M là trung điểm AK

Suy ra: M, A, K thẳng hàng.

c) Gọi H = MA ∩ BC

Vì BEGC là hình thang cân nên ∆BEG = ∆EBC (c–g–c)

⇒ \(\widehat {ECB} = \widehat {EGB}\) mà \(\widehat {EGA} = \widehat {MAG} = \widehat {BAH}\)

⇒ \(\widehat {BAH} + \widehat {ABC} = \widehat {ECB} + \widehat {ABC} = 90^\circ \)

Suy ra: MA vuông góc với BC tại H.

d) Xét ∆ABK và ∆BDC có:

AB = DB

\(\widehat {BAK} = \widehat {DBC}\)

KA = EG = BC

Suy ra: ∆ABK = ∆BDC (c.g.c)

Suy ra: \(\widehat {BKA} = \widehat {BCD}\)

Mà KA ⊥ BC nên CD ⊥ BK

Chứng minh tương tự ta cũng có BF ⊥ KC.

Suy ra: Tam giác KBC có BF, CD, AM là 3 đường cao đồng quy tại trực tâm I.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho ΔABC vuông tại A. Kẻ BD là tia phân giác của \(\widehat {ABC}\)(D ∈ AC). Trên cạnh BC lấy điểm E sao cho BE = BA.

a) Chứng minh ΔABD = ΔEBD.

b) Chứng minh: DE = AD và DE vuông góc với BC.

c) Chứng minh: BD là đường trung trực của đoạn AE.

d) Trên tia đối của tia AB lấy điểm F sao cho AF = CE. Chứng minh ba điểm F, D, E thẳng hàng.

Xem đáp án

Lời giải

Cho tam giác ABC vuông tại A. Kẻ BD là tia phân giác của góc ABC (D thuộc AC) (ảnh 1)

a) Xét tam giác ABD và tam giác EBD có:

AB = BE(gt)

\(\widehat {ABD} = \widehat {EBD}\)(do BD là phân giác \(\widehat {ABD}\))

Cạnh BD chung

Suy ra ΔABD = ΔEBD (c−g−c).

b) Theo câu a) ta có ΔABD = ΔEBD(c−g−c)

Nên DE = AD (hai cạnh tương ứng) và \(\widehat {BED} = \widehat {BAD} = 90^\circ \)(hai góc tương ứng)

Do đó: DE ⊥ BC.

c) Gọi I là giao điểm của BD và AE.

Xét tam giác ABI và tam giác EBI có:

AB = BE (gt)

\(\widehat {ABD} = \widehat {EBD}\) (do BD là phân giác \(\widehat {ABD}\))

Cạnh BI chung

Suy ra ΔABI = ΔEBI (c−g−c).

⇒ IA = IE, \(\widehat {BIA} = \widehat {BIE}\)

Mà \(\widehat {BIA} + \widehat {BIE} = 180^\circ \)(hai góc kề bù)

Nên \(\widehat {BIA} = \widehat {BIE} = 90^\circ \)

Hay BI ⊥ AE

Từ đó ta có BD ⊥ AE tại I và I là trung điểm AE.

Suy ra BD là đường trung trực của đoạn AE.

d) Theo câu b) ta có AD = DE

Xét tam giác ADF và tam giác EDC có:

AD = DE(cmt)

\(\widehat {FAD} = \widehat {DEC} = 90^\circ \)

AF = CE(gt)

Suy ra ΔADF = ΔEDC (c−g−c)

⇒ \(\widehat {ADF} = \widehat {CDF}\)

Mà A, D, C thẳng hàng nên suy ra F, D, E thẳng hàng.

Câu 2

Phép cộng, trừ 2 số cùng số mũ.

Xem đáp án

Lời giải

Không có công thức về cộng, trừ lũy thừa, ta thực hiện phép tính lũy thừa sau đó thực hiện cộng, trừ thông thường.

Ví dụ: 3² – 2² = 9 – 4 = 5

3² – 2² ≠ (3 – 2)² = 1.

Câu 3