Câu hỏi:

19/08/2025 32,820

Cho đường tròn tâm O bán kính R, dây BC khác đường kính. Hai tiếp tuyến của đường tròn (O, R) tại B và tại C cắt nhau tại A. Kẻ đường kính CD, kẻ BH vuông góc với CD tại H.

a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn. Xác định tâm và bán kính của đường tròn đó.

b) Chứng minh AO vuông góc với BC. Cho biết R = 15 cm, BC = 24cm. Tính AB, OA.

c) Chứng minh BC là tia phân giác của góc ABH

d) Gọi I là giao điểm của AD và BH, E là giao điểm của BD và AC. Chứng minh IH = IB.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

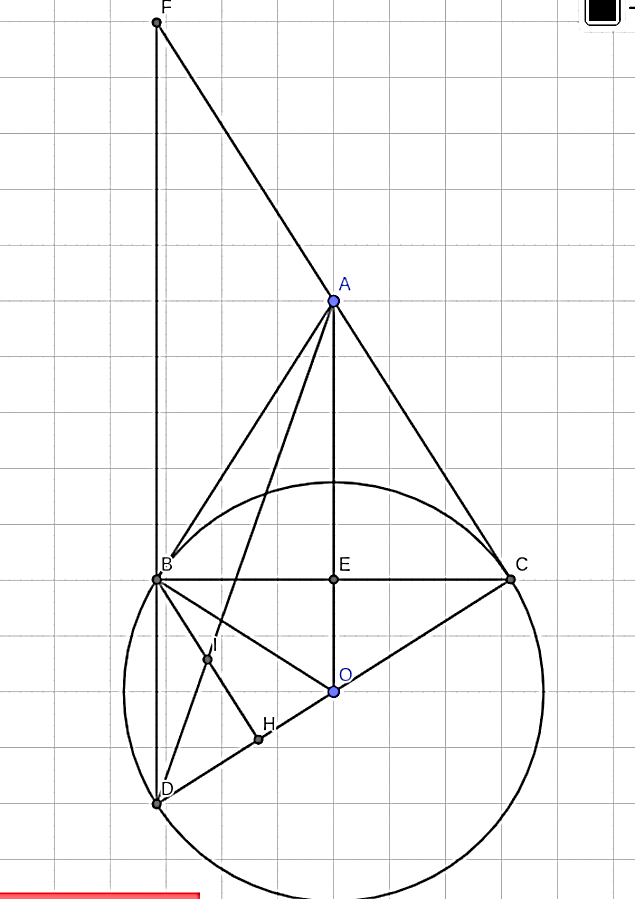
Media VietJack

a) Ta có AB, AC là tiếp tuyến của (O) ⇒ $\hat{A B O} = \hat{A C O}$ = 90°

⇒ $\hat{A B O} + \hat{A C O}$ = 90° + 90° = 180°

⇒ A, B, O, C cùng thuộc đường tròn đường kính (AO).

b) Vì AB, AC là tiếp tuyến của (O)

⇒ AB = AC (tính chất hai tiếp tuyến cắt nhau)

và có OB = OC nên AO là đường trung trực của BC
⇒AO ⊥ BC

Gọi AO ∩ BC = E

⇒ E là trung điểm BC
⇒ BE = $\frac{1}{2} B C$

Do AB ⊥ OB, BE ⊥ AO

Áp dụng hệ thức lượng vào Δ vuông ABO đường cao BE có:

$\frac{1}{B E^{2}} = \frac{1}{O B^{2}} + \frac{1}{B A^{2}}$ ⇒ AB = 20

⇒ OA² = AB² + OB² = 625⇒AO = 25

c) Ta có:
BH ⊥ OC ⇒ BH//AC ⇒ $\hat{H B C} = \hat{A C B} = \hat{A B C}$

⇒ BC là phân giác $\hat{A B H}$

d) Gọi BD ∩ AC = F

Ta có: FB ⊥ BC, AB = AC

⇒ A là trung điểm CF

⇒ AF = AC
Mà BH ⊥ CD

⇒ BH // CF

⇒ $\frac{B I}{A F} = \frac{D I}{D A} = \frac{I H}{A C}$

⇒ IB = IH.

Đang tải chế độ Học...

Hot: 1000+ đề thi cuối kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cách đổi cm³ sang m³.

Xem đáp án

Lời giải

1 cm³ = 10^-3 dm³ = 10^-6 m³ = 0,000001 m³

Như vậy để đổi cm³ sang m³ trên máy tính ta lấy đơn vị cm³ nhân với 10^-6 hoặc chia cho 1000000.

Câu 2

Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?

Xem đáp án

Lời giải

Gọi thời gian tổ I hoàn thành công việc riêng là x (x > 0, giờ),

thời gian tổ II hoàn thành công việc riêng là y (y > 0, giờ)

Trong 1 giờ, tổ I làm được $\frac{1}{x}$ (công việc)

Trong 1 giờ, tổ II làm được $\frac{1}{y}$ (công việc)

Trong 1 giờ, cả 2 tổ làm được $\frac{1}{6}$ (công việc)

Nên ta có phương trình: $\frac{1}{x} + \frac{1}{y} = \frac{1}{6}$ (1)

Trong 10 giờ, tổ I làm được $\frac{10}{x}$ (công việc)

Vì sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I hoàn thành công việc còn lại trong 10 giờ nên ta có phương trình: $2 (\frac{1}{x} + \frac{1}{y}) + \frac{10}{x} = 1$

⇔ 2. $\frac{1}{6}$ + $\frac{10}{x}$ = 1

⇔ x = 15

Thay vào (1) tìm được y = 10

Vậy thời gian tổ I hoàn thành công việc riêng là 15 giờ.

thời gian tổ II hoàn thành công việc một mình là 10 giờ.

Câu 3