Câu hỏi:
12/07/2024 751
Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2kg nguyên liệu và 30 giờ, đem lại mức lời 40000 đồng. Mỗi kg sản phẩm loại II cần 4kg nguyên liệu và 15giờ, đem lại mức lời 30000 đồng. Xưởng có 200kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm lần lượt là bao nhiêu để có mức lời cao nhất?
Quảng cáo
Trả lời:
Giải bởi Vietjack
+ Gọi x (x ≥ 0) là số kg loại I cần sản xuất, y (y ≥ 0) là số kg loại II cần sản xuất.
Suy ra số nguyên liệu cần dùng là 2x + 4y, thời gian là 30x + 15y có mức lời là 40 000x + 30 000y
Theo giả thiết bài toán xưởng có 200kg nguyên liệu và 1200 giờ làm việc suy ra
2x + 4y ≤ 200 hay x + 2y – 100 ≤ 0 ; 30x + 15y ≤ 1200 hay 2x+ y – 80 ≤ 0
+ Tìm x; y thoả mãn hệ (*)
sao cho L(x; y) = 40 000x + 30 000y đạt giá trị lớn nhất.
Trong mặt phẳng tọa độ vẽ các đường thẳng (d): x + 2y – 100= 0 và (d’) : 2x + y – 80 = 0
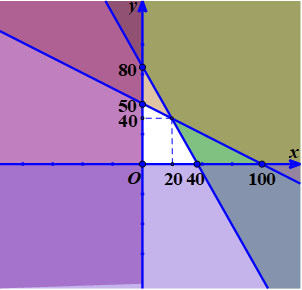
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tứ giác) không tô màu trên hình vẽ
Giá trị lớn nhất của L( x; y) đạt tại một trong các điểm (0; 0) ; (40; 0) ; (0; 50) ; (20; 40)
+ Ta có L(0; 0) = 0; L( 40; 0) = 1 600 000;
L(0; 50) = 1 500 000; L(20; 40) = 2 000 000
Suy ra giá trị lớn nhất của L(x; y) là 2 000 000 khi (x; y) = (20; 40).
Vậy cần sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II để có mức lời lớn nhất.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?
Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?
Xem đáp án »
12/07/2024
51,594
Câu 4:
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá triệu đồng có thể chiết xuất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại
Xem đáp án »
12/07/2024
40,303
Câu 5:
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
Xem đáp án »
13/07/2024
35,961
Câu 6:
Trong một giỏ hoa có 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa coi như đôi một khác nhau). Người ta muốn làm một bó hoa gồm 7 bông được lấy từ giỏ hoa đó. Hỏi có bao nhiêu cách chọn hoa biết bó hoa có đúng 1 bông hồng đỏ?
Trong một giỏ hoa có 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa coi như đôi một khác nhau). Người ta muốn làm một bó hoa gồm 7 bông được lấy từ giỏ hoa đó. Hỏi có bao nhiêu cách chọn hoa biết bó hoa có đúng 1 bông hồng đỏ?
Xem đáp án »
12/07/2024
33,326
Câu 7:
Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi .
Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi .
Xem đáp án »
13/07/2024
32,190
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận