Câu hỏi:
12/07/2024 3,828
Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
a) Chứng minh rằng: AD = MN; = 90°.
b) Gọi AH vuông góc BC tại H. Chứng minh rằng: = 90°.
c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?
Cho tam giác ABC vuông tại A. Điểm D thuộc cạnh BC. Gọi M, N theo thứ tự là hình chiếu của D tại AB, AC.
a) Chứng minh rằng: AD = MN; = 90°.
b) Gọi AH vuông góc BC tại H. Chứng minh rằng: = 90°.
c) Khi D chuyển động trên BC thì trung điểm I của MN chuyển động trên đường nào?
Quảng cáo
Trả lời:
Giải bởi Vietjack
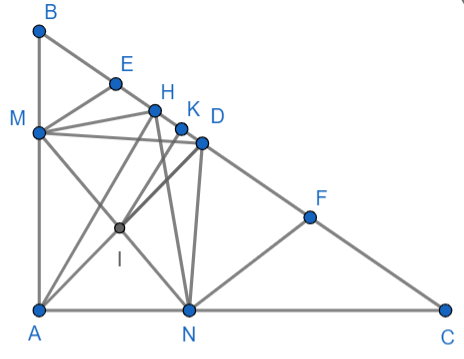
a) Ta có: = 90°
Nên AMDN là hình chữ nhật
Suy ra: AD = MN; = 90°
b) Gọi I là trung điểm của MN và AD
HI là đường trung tuyến của ∆HAD vuông tại H suy ra: HI =
Mà AD = MN nên HI =
Mà HI là đường trung tuyến của ∆HMN (I là trung điểm MN)
Nên ∆HMN vuông tại H
Suy ra: = 90°
c) Kẻ IK vuông góc HD
Ta có: AH ⊥ HD nên IK // AH
Mà I là trung điểm AD nên IK là đường trung bình của tam giác DAH
Suy ra: IK =
Điểm I cách đoạn thẳng BC 1 khoảng cố định bằng một nửa AH không đổi.
Vậy I di chuyển trên đường thẳng song song với BC và cách BC 1 khoảng bằng nửa AH.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới)
Đã bán 1,5k
₫ 70.000
₫ 36.000
Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025)
Đã bán 1,1k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?
Để hoàn thành một công việc hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc?
Xem đáp án »
12/07/2024
51,594
Câu 4:
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá triệu đồng có thể chiết xuất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại
Xem đáp án »
12/07/2024
40,302
Câu 5:
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC , trên tia đối của tia MB lấy điểm D sao cho MD = MB.
1) Chứng minh AD = BC.
2) Chứng minh CD vuông góc với AC.
3) Đường thẳng qua B song song với AC cắt tia DC tại N. Chứng minh ∆ABM = ∆CNM.
Xem đáp án »
13/07/2024
35,961
Câu 6:
Trong một giỏ hoa có 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa coi như đôi một khác nhau). Người ta muốn làm một bó hoa gồm 7 bông được lấy từ giỏ hoa đó. Hỏi có bao nhiêu cách chọn hoa biết bó hoa có đúng 1 bông hồng đỏ?
Trong một giỏ hoa có 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa coi như đôi một khác nhau). Người ta muốn làm một bó hoa gồm 7 bông được lấy từ giỏ hoa đó. Hỏi có bao nhiêu cách chọn hoa biết bó hoa có đúng 1 bông hồng đỏ?
Xem đáp án »
12/07/2024
33,326
Câu 7:
Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi .
Chứng minh điểm G là trọng tâm của tam giác ABC khi và chỉ khi .
Xem đáp án »
13/07/2024
32,186
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận