Câu hỏi:
20/09/2023 962
Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng \[\frac{a}{6}\]Thể tích khối lăng trụ bằng
Mệnh đề nào đúng?
Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng \[\frac{a}{6}\]Thể tích khối lăng trụ bằng
Mệnh đề nào đúng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
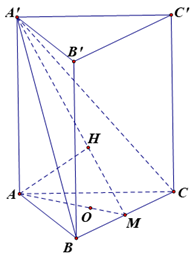
Gọi M là trung điểm của BC và H là hình chiếu của A trên A’M.
Ta có :
\(\left. {\begin{array}{*{20}{c}}{BC \bot AM}\\{BC \bot AA'}\end{array}} \right\}\) ⇒ BC ⊥ (AA’M) ⇒ BC ⊥ AH (1).
Mà AH ⊥ A’M (2).
Từ (1) và (2) ⇒ d(A, (A’BC)) = AH.
Ta có: \(\frac{{d\left( {O,\left( {A'BC} \right)} \right)}}{{d\left( {A,\left( {A'BC} \right)} \right)}} = \frac{{MO}}{{MA}} = \frac{1}{3}\) (do tính chất trọng tâm).
\( \Rightarrow d\left( {A,\left( {A'BC} \right)} \right) = 3d\left( {O,\left( {A'BC} \right)} \right) = \frac{a}{2}\)
\( \Rightarrow AH = \frac{a}{2}\)
Xét tam giác vuông A'AM :
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{A^{{\rm{'}}2}}}} + \frac{1}{{A{M^2}}}\)
\( \Leftrightarrow \frac{1}{{A{A^{{\rm{'}}2}}}} = \frac{4}{{{a^2}}} - \frac{4}{{3{a^2}}} \Leftrightarrow AA' = \frac{{a\sqrt 3 }}{{2\sqrt 2 }}\)
Suy ra thể tích lăng trụ ABC.A’B’C’ là:
\(V = AA' \cdot {S_{\Delta ABC}} = \frac{{a\sqrt 3 }}{{2\sqrt 2 }} \cdot \frac{{{a^2}\sqrt 3 }}{4} = \frac{{3\sqrt 2 {a^3}}}{{16}}.\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: A
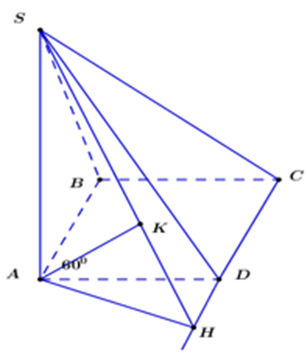
Ta có: AB // (SCD)
⇒ d(B; (SCD)) = d(A; (SCD)) = d
Kẻ AH ⊥ CD; AK ⊥ SH
\(\left\{ {\begin{array}{*{20}{c}}{CD \bot SA}\\{CD \bot AH}\end{array} \Rightarrow CD \bot \left( {SAH} \right)} \right.\)
⇒ CD ⊥ AK ⇒ AK ⊥ (SCD)
⇒ d(B; (SCD)) = d = AK.
Xét ∆AHD vuông tại H, \[\widehat {ADH} = 60^\circ \]
ta có: \(AH = AD \cdot {\rm{sin}}60^\circ = \frac{{a\sqrt 3 }}{2}\)
Áp dụng hệ thức lượng trong tam giác vuông SHA vuông tại A có đường cao AK ta có: \(AK = \frac{{SA \cdot AH}}{{\sqrt {S{A^2} + A{H^2}} }}\)\( = \frac{{a \cdot \frac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + \frac{{3{a^2}}}{4}} }} = \frac{{a\sqrt {21} }}{7} = d.\)
Lời giải
Đáp án đúng là: B
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ta có:
\(\frac{{x - 3}}{{x - 2}} + \frac{{x - 2}}{{x - 1}} + \frac{{x - 1}}{x} + \frac{x}{{x + 1}} = \left| {x + 2} \right| - x + m\)
\( \Leftrightarrow \frac{{x - 3}}{{x - 2}} + \frac{{x - 2}}{{x - 1}} + \frac{{x - 1}}{x} + \frac{x}{{x + 1}} - \left| {x + 2} \right| + x = m\)
Xét hàm số \(f\left( x \right) = \frac{{x - 3}}{{x - 2}} + \frac{{x - 2}}{{x - 1}} + \frac{{x - 1}}{x} + \frac{x}{{x + 1}} - \left| {x + 2} \right| + x\) có TXĐ: D = ℝ ∖ {‒1; 0; 1; 2}.
\(f'\left( x \right) = \frac{1}{{{{(x - 2)}^2}}} + \frac{1}{{{{(x - 1)}^2}}} + \frac{1}{{{x^2}}} + \frac{1}{{{{(x + 1)}^2}}} - \frac{{x + 2}}{{\left| {x + 2} \right|}} + 1\)
\( = \frac{1}{{{{(x - 2)}^2}}} + \frac{1}{{{{(x - 1)}^2}}} + \frac{1}{{{x^2}}} + \frac{1}{{{{(x + 1)}^2}}} + \frac{{\left| {x + 2} \right| - \left( {x + 2} \right)}}{{\left| {x + 2} \right|}}\)
\( \Rightarrow f'\left( x \right) > 0\forall x \in D\)
Do \(\left| {x + 2} \right| \ge x + 2\forall x \Rightarrow \left| {x + 2} \right| - \left( {x + 2} \right) \ge 0 \Leftrightarrow \frac{{\left| {x + 2} \right| - \left( {x + 2} \right)}}{{\left| {x + 2} \right|}} \ge 0\)
\( \Rightarrow f'\left( x \right) > 0\forall x \in D \Rightarrow \) Hàm số đồng biến trên từng khoảng xác định của nó.
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy phương trình f(x) = m có đúng 4 nghiệm phân biệt khi và chỉ khi m ≥ 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận