Tam giác ABC có độ dài AB = 4 cm, AC = 6 cm, BC = 9 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 66,5 cm. Hãy tính độ dài các cạnh của tam giác A'B'C'.
Quảng cáo
Trả lời:
Lời giải:
Chu vi tam giác ABC: AB + AC + BC = 19.
Tỉ số chu vi của hai tam giác ABC và A'B'C' là: \[k = \frac{{19}}{{66,5}} = \frac{2}{7}\].
ΔABC ᔕ ΔA′B′C′ nên \[\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{2}{7}\].
Vậy: A′B′=14, A′C′=21, \[B'C' = \frac{{63}}{2}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
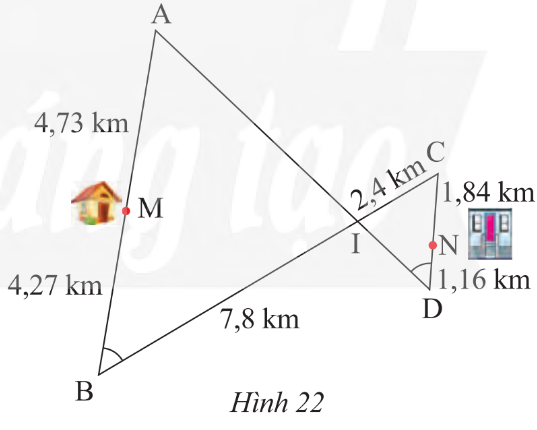
Xét ΔIAB và ΔICD ta có:
\[\widehat B = \widehat {D\;}\] (gt)
\[\widehat {AIB} = \widehat {CID}\] (đối đỉnh)
Suy ra ΔIAB ᔕ ΔICD (g.g) nên \[\frac{{IA}}{{TC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}}\]
\[ \Rightarrow \frac{{IA}}{{2,4}} = \frac{{7,8}}{{ID}} = \frac{9}{3} = 3\;\] ⇒ IA = 7,2; ID = 2,6
Quãng đường đi từ M → A → I là: 4,73 + 7,2 = 11,93 (km)
Quãng đường đi từ M → B → I là: 4,27 + 7,8 = 12,07 (km)
Quãng đường đi từ I → C → N là: 2,4 + 1,84 = 4,24 (km)
Quãng đường đi từ I → D → N là: 2,6 + 1,16 = 3,76 (km)
Vậy quãng đường ngắn nhất để đi từ nhà của anh Thanh đến công ty là M → A → I → D → N với độ dài 15,69 km.
Lời giải
Lời giải:
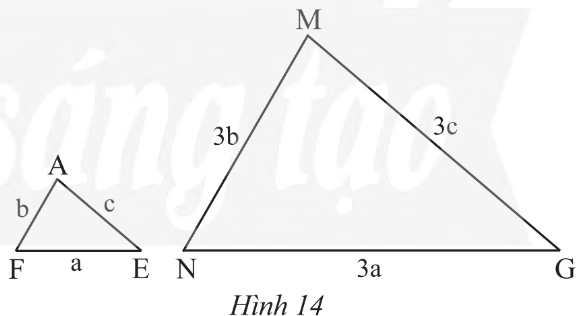
a) Xét ∆AFE và ∆MNG có:
\[\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\;\frac{{FE}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3};\;\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3}\].
Suy ra \[\frac{{AF}}{{MN}} = \frac{{FE}}{{NG}} = \;\frac{{AE}}{{MG}}\].
Vậy ΔAFE ᔕ ΔMNG (c.c.c).
b) Tam giác AFE đồng dạng với tam giác MNG theo tỉ số \[\frac{1}{3}\] nên tỉ số chu vi của hai tam giác đó cũng bằng \[\frac{1}{3}\].
Vậy chu vi tam giác MNG là: 15.3 = 45 (cm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.