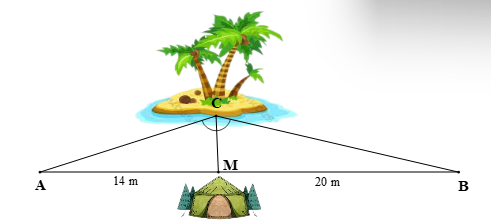
Để bảo trì tượng nữ thần tự do với chiều cao là AD = 93 m người thợ đã gắn hai dây thép cố định vào hai vị trí B và C (như hình vẽ) sao cho Tính chiều dài của dây thép khi được căng thẳng từ A đến B biết rằng độ dài BC = 20 m và CD = 15 m

Quảng cáo
Trả lời:
Đáp án đúng là: B
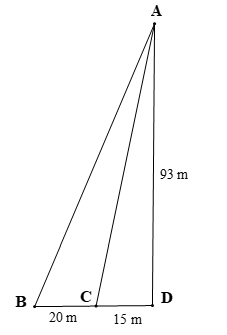
Do nên AC là đường phân giác của
Xét ∆BAD có AC là đường phân giác của nên áp dụng tính chất đường phân giác trong ∆BAD ta có:
⇒ AB ∙ 15 = 20 ∙ 93 ⇒ AB ∙ 15 = 1 860
(m).
Vậy chiều dài của dây thép khi được căng thẳng từ A đến B là 124 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: A
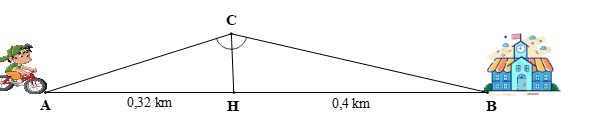
Thời gian để bạn Hải đi từ A đến C là: 6 giờ 30 phút – 6 giờ = 30 phút = 0,5 giờ.
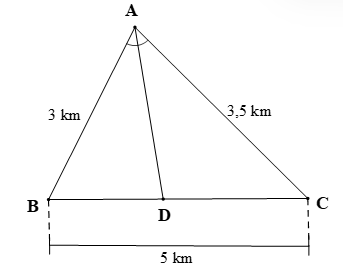
Quãng đường mà bạn Hải đi từ A đến C trong 0,5 giờ với tốc độ trung bình lên dốc 4 km/h là: AC = SA→C = 4 ∙ 0,5 = 2 (km).
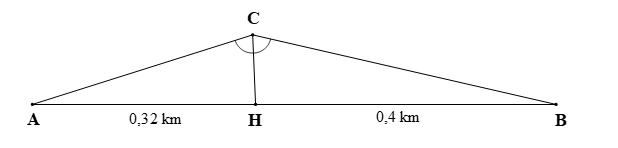
Xét ∆ACB có CH là đường phân giác của nên áp dụng tính chất đường phân giác trong ∆ACB ta có:
⇒ 0,32 ∙ CB = 0,4 ∙ 2 ⇒ 0,32 ∙ CB = 0,8
(m).
Thời gian để bạn Hải đi hết quãng đường CB = 2,5 m với tốc độ trung bình xuống dốc 10 km/h là: (giờ).
Như vậy, tổng thời gian bạn Hải đi từ A đến trường B là
0,5 + 0,25 = 0,75 (giờ) = 45 (phút).
Do đó bạn Hải đến trường lúc 6 giờ 45 phút.
Câu 2
Lời giải
Đáp án đúng là: A
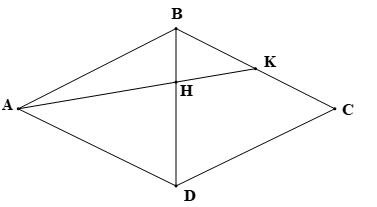
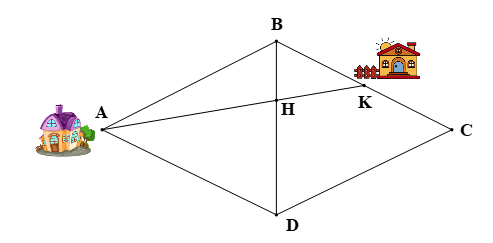
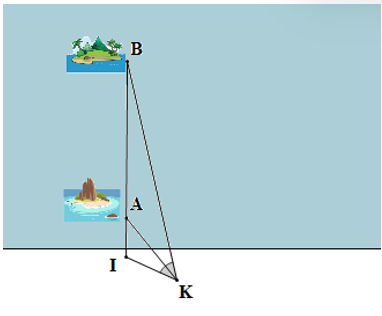
Theo đề bài, ABCD là hình thoi nên BA = BC và BD là tia phân giác của
Vì K là trung điểm của BC nên
Xét ∆ABK có: BH là tia phân giác của (do BD là tia phân giác của ).
Áp dụng tính chất đường phân giác trong ∆ABK với BH là tia phân giác của ta có:
Theo đề bài, H là địa điểm gặp nhau nên bạn Hoa đi theo quãng đường KH, bạn Phương đi theo quãng đường AH.
Ta có: S = vt, mà quãng đường bạn Phương đi bằng 2 lần quãng đường bạn Hoa đi và vận tốc đi xe đạp của hai bạn đều bằng nhau nên thời gian bạn Phương đi bằng 2 lần thời gian bạn Hoa đi thì hai bạn mới gặp nhau tại địa điểm H.
Bạn Phương gặp bạn Hoa lúc 8 giờ 15 phút và Hoa xuất phát lúc 8 giờ nên thời gian bạn Hoa đi hết quãng đường KH là:
8 giờ 15 phút – 8 giờ = 15 phút.
Khi đó, thời gian bạn Phương đi là 2 ∙ 15 = 30 (phút).
Do đó, bạn Phương phải xuất phát từ lúc: 8 giờ 15 phút – 30 phút = 7 giờ 45 phút.
Vậy bạn Phương phải xuất phát lúc 7 giờ 45 phút giờ để gặp bạn Hoa lúc 8 giờ 15 phút tại điểm H.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 7 giờ;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
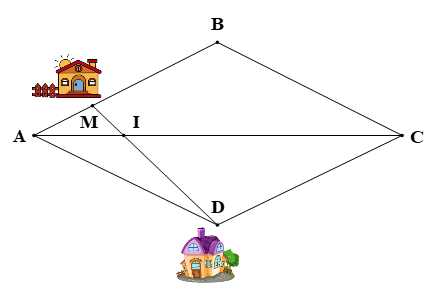
Ba bạn Mai, Lan, Điệp hẹn gặp nhau tại nhà bạn Lan, biết rằng nhà bạn Mai ở vị trí A, nhà bạn Lan ở vị trí G và nhà bạn Điệp ở vị trí M (được mô tả như hình vẽ). Biết rằng tứ giác ABCD là hình vuông và M là trung điểm của CD. Quãng đường bạn Điệp đi từ nhà tới nhà bạn Lan là 3 km. Hỏi bạn Mai phải đi quãng đường ngắn nhất từ nhà tới nhà bạn Lan là bao nhiêu kilômét để gặp Lan và Điệp?
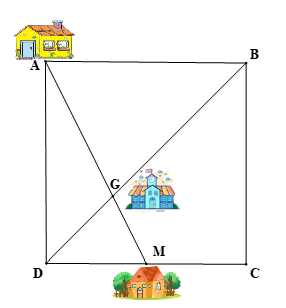
Ba bạn Mai, Lan, Điệp hẹn gặp nhau tại nhà bạn Lan, biết rằng nhà bạn Mai ở vị trí A, nhà bạn Lan ở vị trí G và nhà bạn Điệp ở vị trí M (được mô tả như hình vẽ). Biết rằng tứ giác ABCD là hình vuông và M là trung điểm của CD. Quãng đường bạn Điệp đi từ nhà tới nhà bạn Lan là 3 km. Hỏi bạn Mai phải đi quãng đường ngắn nhất từ nhà tới nhà bạn Lan là bao nhiêu kilômét để gặp Lan và Điệp?

A. 12 km;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.