Cho hai hình hộp chữ nhật bằng nhau cùng có thể tích 200 cm3 và một hình hộp chữ nhật có thể tích 500 cm3 sắp xếp như trong hình bên (độ dài các cạnh hình hộp được tính bằng đơn vị cm). Viết các phân...

Câu hỏi:

13/07/2024 1,738

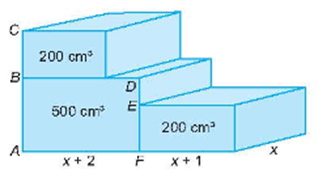
Cho hai hình hộp chữ nhật bằng nhau cùng có thể tích 200 cm³ và một hình hộp chữ nhật có thể tích 500 cm³ sắp xếp như trong hình bên (độ dài các cạnh hình hộp được tính bằng đơn vị cm). Viết các phân thức biểu thị độ dài (tính bằng cm) của các đoạn thẳng AC và DE.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 8 KNTT Phép cộng và phép trừ phân thức đại số có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi y (cm) là độ dài đoạn thẳng DE. (y > 0).

Ta có: AB = DE + EF

Vì hình hộp chữ nhật 200 cm³ có diện tích đáy là: (x + 1)x (cm²), từ đó suy ra chiều cao EF = \(\frac{{200}}{{x\left( {x + 1} \right)}}\) (cm).

Vì hình hộp chữ nhật 500 cm³ có diện tích đáy là: (x + 2)x (cm²), từ đó suy ra chiều cao AB = \(\frac{{500}}{{x\left( {x + 2} \right)}}\) (cm).

Vì AB = DE + EF

Suy ra DE = AB – EF = \(\frac{{500}}{{x\left( {x + 2} \right)}}\) – \(\frac{{200}}{{x\left( {x + 1} \right)}}\)

= \(\frac{{500\left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}} - \frac{{200\left( {x + 2} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)

= \(\frac{{500\left( {x + 1} \right) - 200\left( {x + 2} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)

\( = \frac{{500x + 500 - 200x - 400}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)

\( = \frac{{300x + 100}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\).

Ta lại có:

CB = EF = \(\frac{{200}}{{x\left( {x + 1} \right)}}\) (cm) (vì hai hình hộp chữ nhật bằng nhau có cùng thể tích 200 cm²).

AC = CB + AB = \(\frac{{200}}{{x\left( {x + 1} \right)}}\) + \(\frac{{500}}{{x\left( {x + 2} \right)}}\)

= \(\frac{{500\left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{{200\left( {x + 2} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)

= \(\frac{{500\left( {x + 1} \right) + 200\left( {x + 2} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)

\( = \frac{{500x + 500 + 200x + 400}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)

\( = \frac{{700x + 900}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\).

Vậy phân thức biểu diễn độ dài độ dài các đoạn thẳng DE và AC là

DE =\(\frac{{300x + 100}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\) (cm) và AC = \(\frac{{700x + 900}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\) (cm).

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tính:

\(\frac{{5x + {y^2}}}{{{x^2}y}} - \frac{{5y - {x^2}}}{{x{y^2}}}\);

Xem đáp án

Lời giải

\(\frac{{5x + {y^2}}}{{{x^2}y}} - \frac{{5y - {x^2}}}{{x{y^2}}}\)

\( = \frac{{y\left( {5x + {y^2}} \right)}}{{{x^2}{y^2}}} - \frac{{x\left( {5y - {x^2}} \right)}}{{{x^2}{y^2}}}\) (Mẫu thức chung là: x²y²)

\( = \frac{{5xy + {y^3}}}{{{x^2}{y^2}}} - \frac{{5xy - {x^3}}}{{{x^2}{y^2}}}\)

\( = \frac{{5xy + {y^3} - 5xy + {x^3}}}{{{x^2}{y^2}}} = \frac{{{x^3} + {y^3}}}{{{x^2}{y^2}}}\).

Câu 2

Rút gọn biểu thức \(P = \frac{{{x^2} + 2x}}{{{x^3} - 1}} - \frac{1}{{{x^2} - x}} - \frac{1}{{{x^2} + x + 1}}\) (x ≠ 0, x ≠ 1).

Xem đáp án

Lời giải

Ta có:

\(P = \frac{{{x^2} + 2x}}{{{x^3} - 1}} - \frac{1}{{{x^2} - x}} - \frac{1}{{{x^2} + x + 1}}\) (x ≠ 0, x ≠ 1)

\( = \frac{{{x^2} + 2x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{1}{{x\left( {x - 1} \right)}} - \frac{1}{{{x^2} + x + 1}}\)

\( = \frac{{\left( {{x^2} + 2x} \right)x}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{{{x^2} + x + 1}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} - \frac{{x\left( {x - 1} \right)}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{\left( {{x^2} + 2x} \right)x - \left( {{x^2} + x + 1} \right) - x\left( {x - 1} \right)}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{{x^3} + 2{x^2} - {x^2} - x - 1 - {x^2} + x}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)\( = \frac{{{x^3} - 1}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)

\( = \frac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{x\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)\( = \frac{1}{x}\).

Câu 3