Câu hỏi:

19/08/2025 661

Cho tam giác ABC có đường cao AH và BD cắt nhau tại I.

a) Chứng minh 4 điểm C, D, I, H cùng thuộc 1 đường tròn.

b) Chứng minh 4 điểm A, B, H, D cùng thuộc 1 đường tròn.

c) Tính bán kính đường tròn đi qua 4 điểm C, D, H, I nếu biết CH = 4cm và $\hat{H A B}$ = 30°.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

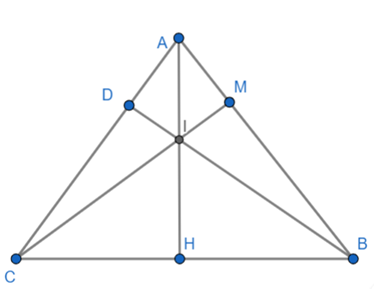
Cho tam giác ABC có đường cao AH và BD cắt nhau tại I. a) Chứng minh 4 điểm C, D, I, H cùng thuộc 1 đường tròn. b) Chứng minh 4 điểm A, B, H, D cùng thuộc 1 đường tròn. (ảnh 1)

a) Xét tam giác DIC vuông tại D (BD ⊥ AC)

⇒ D, I, C cùng thuộc đường tròn đường kính IC

Xét tam giác HIC vuông tại H (AH ⊥ BC)

⇒ H, I, C cùng thuộc đường tròn đường kính IC

Vậy D, I, C, H cùng thuộc đường tròn đường kính IC

b) Xét tam giác ABH vuông tại H (AH ⊥ BC)

⇒ A, B, H cùng thuộc đường tròn đường kính AB

Xét tam giác ABD vuông tại D (BD ⊥ AC)

⇒ A, B, D cùng thuộc đường tròn đường kính AB

Vậy A, B, H, D cùng thuộc đường tròn đường kính AB

c) Gọi M là giao điểm của CI và AB

Xét tam giác BAC có: AH và BD là đường cao, AH ∩ BD ={I}

Nên I là trực tâm của tam giác BAC

Vậy AM là đường cao thứ 3 của tam giác ABC

Xét ∆ABH và ∆CBM có:

$\hat{B}$ chung

$\hat{A H B} = \hat{C M B} = 90 °$

⇒ ∆ABH ~ ∆CBM (g.g)

⇒ $\hat{B C M} = \hat{H A B}$ = 30°

Xét ∆HCI vuông tại H có: cos $\hat{H C I} = \frac{C H}{C I} \Rightarrow \cos 30 ° = \frac{4}{C I} \Rightarrow C I = \frac{8 \sqrt{3}}{3} (c m)$

Mà đường tròn đi qua D, I, C, H là đường tròn đường kính IC

Suy ra bán kính đường tròn là $\frac{1}{2} C I = \frac{4 \sqrt{3}}{3} (c m) .$

Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC cân tại A lấy điểm D bất kì trên AB, lấy điểm E trên tia đối của tia CA sao cho CE = BD. Từ D kẻ đường thẳng song song với AC cắt BC tại F

a) Tam giác DBF là tam giác gì?

b) Chứng minh tứ giác DCEF là hình bình hành.

Xem đáp án

Lời giải

Cho tam giác ABC cân tại A lấy điểm D bất kì trên AB, lấy điểm E trên tia đối của tia CA sao cho CE = BD. Từ D kẻ đường thẳng song song với AC cắt BC tại F (ảnh 1)

a) Ta có: DF // AC nên: $\hat{D F B} = \hat{A C B} = \hat{B}$

Suy ra: tam giác DBF cân tại D

b) Từ câu a ta có: DB = DF

Mà DB = CE theo giả thiết nên DF = CE

Lại có: DF // AC nên DF // CE

Xét tứ giác DCEF có: DF // CE và DF = CE

Vậy DCEF là hình bình hành.

Câu 2

Cho tam giác vuông ABC vuông ở A có đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB và AC.

a. So sánh AH và EF.

b. Tính độ dài HF biết AB = 6 cm, BC = 10 cm và BH = 3,6 cm.

Xem đáp án

Lời giải

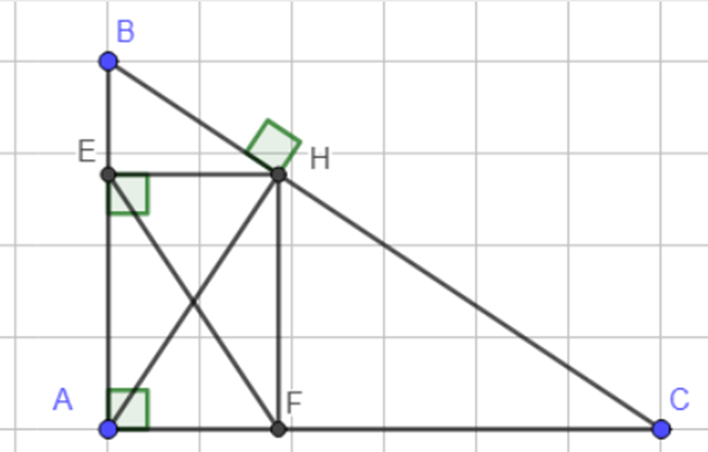
Cho tam giác vuông ABC vuông ở A có đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB và AC. a. So sánh AH và EF. b. Tính độ dài HF biết AB = 6 cm, BC = 10 cm và BH = 3,6 cm. (ảnh 1)

a) Xét tứ giác AEHF có: $\hat{A} = \hat{E} = \hat{F} = 90 °$

Nên AEHF là hình chữ nhật

Suy ra: AH = EF

b) Xét tam giác AHE và tam giác AHB có:

$\hat{A}$ chung

$\hat{A E H} = \hat{A H B} = 90 °$

⇒ ∆AEH ∽ ∆AHB (g.g)

⇒ $\frac{A E}{A H} = \frac{A H}{A B}$

⇒ AE = $\frac{A H^{2}}{A B} = \frac{A B^{2} - B H^{2}}{A B} = \frac{6^{2} - 3, 6^{2}}{6} = 3, 84 (c m)$ .

Câu 3