1) Giải hệ phương trình $\left\{\begin{array}{l}\frac{2}{x-3}-3y=1\\ \frac{3}{x-3}+2y=8\end{array}\right..$

2) Trong mặt phẳng toạ độ Oxy, cho parabol $\left(P\right):y=x^2$ và đường thẳng $\left(d\right):y=\left(m+2\right)x-m.$

a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt.

b) Gọi $x_1$ và $x_2$ là hoành độ các giao điểm của (d) và (P). Tìm tất cả giá trị của m để $\frac{1}{x_1}+\frac{1}{x_2}=\frac{1}{x_1+x_2-2}.$

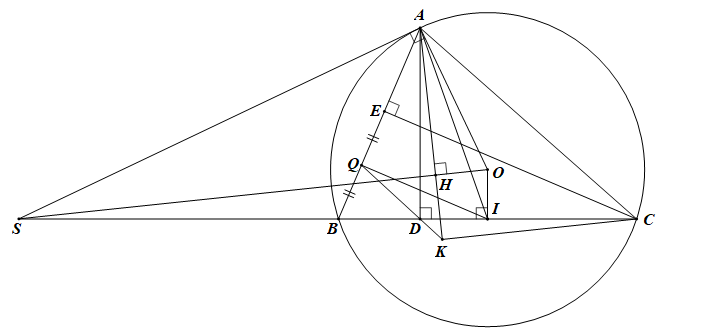
1) Có SA là tiếp tuyến nên $SA\perp OA$$\Rightarrow \widehat{SAO}=90°.$

Vì $OI\perp BC\left(gt\right)\Rightarrow \widehat{SIO}=90°.$

Tứ giác SAOI có $\widehat{SAO}+\widehat{SIO}=90°+90°=180°,$ mà hai góc này ở vị trí đối nhau nên SAOI là tứ giác nội tiếp.

Vì SAOI là tứ giác nội tiếp nên $\widehat{SOA}=\widehat{SIA}$ (hai góc nội tiếp cùng chắn cung SA) hay $\widehat{AOH}=\widehat{AID}\left(1\right)$

$\text{Δ}AHO$ vuông tại $H\left(AH\perp SO\right)$ nên $\widehat{AOH}+\widehat{OAH}=90°\Rightarrow \widehat{OAH}=90°-\widehat{AOH}\left(2\right)$

$\text{Δ}ADI$ vuông tại $H\left(AD\perp SC\right)$ nên $\widehat{AID}+\widehat{IAD}=90°\Rightarrow \widehat{IAD}=90°-\widehat{AID}\left(3\right)$

Từ (1), (2) và (3) ta có $\widehat{OAH}=\widehat{IAD}.$

3) * Chứng minh $BQ\cdot BA=BD\cdot BI.$

Cách 1: Xét tứ giác AEDC có $\widehat{AEC}=\widehat{ADC}=90°,$ mà hai góc này cùng nhìn cạnh AC

Do đó tứ giác AEDC nội tiếp suy ra $\widehat{AED}+\widehat{DCA}=180°.$

Mà $\widehat{AED}+\widehat{BED}=180°$ (kề bù), suy ra $\widehat{BED}=\widehat{DCA}.$

Xét $\Delta BED$ và $\Delta BCA$ có: $\widehat{ABC}$ chung và $\widehat{BED}=\widehat{BCA}.$

Do đó $\Delta BED\backsim \Delta BCA$ (g.g) $\Rightarrow \frac{BE}{BC}=\frac{BD}{BA}$ (tỉ số đồng dạng).

$\Rightarrow BD\cdot BC=BE\cdot BA$$\Rightarrow \frac{1}{2}BC\cdot BD=\frac{1}{2}BE\cdot BA$$\Rightarrow BI\cdot BD=BQ\cdot BA.$

Suy ra tứ giác QDIA nội tiếp.

Cách 2: Xét $\Delta BCE$ có Q, I lần lượt là trung điểm của BE, BC nên QI là đường trung bình của tam giác.

$\Rightarrow QI\text{\hspace{0.17em}//\hspace{0.17em}}EC,$ mà $AB\perp EC$ nên $AB\perp QI$ hay $\widehat{AQI}=90°.$

Xét tứ giác AQDI có $\widehat{AQI}=\widehat{ADI}=90°,$ mà hai góc này cùng nhìn cạnh AI.

Do đó tứ giác AQDI nội tiếp $\Rightarrow BQ\cdot BA=BI\cdot BD.$

* Chứng minh $CK\text{\hspace{0.17em}//\hspace{0.17em}}SO.$

Ta có $\widehat{BAD}=90°-\widehat{ABC}=90°-\frac{\widehat{AOC}}{2}=\widehat{OAC}.$

Mà $\widehat{IAD}=\widehat{OAH}$ (theo câu b) nên $\widehat{BAI}=\widehat{KAC}.$

Lại có tứ giác AQDI nội tiếp nên $\widehat{BDQ}=\widehat{BAI}=\widehat{KAC}.$

Mặt khác $\widehat{CDK}=\widehat{BDQ},$ do đó $\widehat{CDK}=\widehat{KAC}.$

Suy ra tứ giác ADKC nội tiếp nên $\widehat{CKA}=\widehat{CDA}=90°\Rightarrow CK\perp AK.$

Mà $AK\perp SO$ nên $CK\text{\hspace{0.17em}//\hspace{0.17em}}SO.$

1) Gọi số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là x (sản phẩm) $\left(x\in {\mathbb{N}}^{\text{*}},x<900\right).$

Do đó, theo kế hoạch, thời gian phân xưởng làm xong 900 sản phẩm là $\frac{900}{x}$ (ngày).

Thực tế, mỗi ngày, phân xưởng đã làm được nhiều hơn 15 sản phẩm so với số sản phẩm phải làm trong một ngày theo kế hoạch nên thực tế, số sản phẩm mỗi ngày phân xưởng phải làm là $x+15$ (sản phẩm).

Do đó, thực tế, thời gian phân xưởng làm xong 900 sản phẩm là$\frac{900}{x+15}$ (ngày).

Vì phân xưởng đã làm xong 900 sản phẩm 3 ngày trước khi hết thời hạn nên ta có phương trình: $\frac{900}{x+15}+3=\frac{900}{x}$

$\iff \frac{900}{x}-\frac{900}{x+15}=3$$\iff \frac{1}{x}-\frac{1}{x+15}=\frac{1}{300}$

$\iff \frac{x+15-x}{x\left(x+15\right)}=\frac{1}{300}$$\iff \frac{15}{x^2+15x}=\frac{1}{300}$

$\Rightarrow x^2+15x=4500$$\iff x^2+15x-4500=0$

$\iff \left(x-60\right)\left(x+75\right)=0$$\iff \left[\begin{array}{l}x=60\\ x=-75\end{array}\right..$

Đối chiếu điều kiện và thử lại ta thấy $x=60$ thỏa mãn.

Vậy số sản phẩm mỗi ngày phân xưởng phải làm theo kế hoạch là 60 sản phẩm.

2) Thể tích khối gỗ là $V=\pi R^{2}h\approx \mathrm{3,14}\cdot {30}^2\cdot 120=339120\left({\text{cm}}^3\right).$

Vậy $V\approx 339120{\text{ cm}}^3.$