Cho tam giác ABC có đường cao AH = 6 cm, Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét)
Cho tam giác ABC có đường cao AH = 6 cm, Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét)
Quảng cáo
Trả lời:
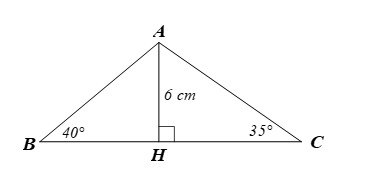
Xét ∆ABH vuông tại H, ta có:
⦁ suy ra
⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).
Xét ∆ACH vuông tại H, ta có:
⦁ suy ra
⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm).
Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
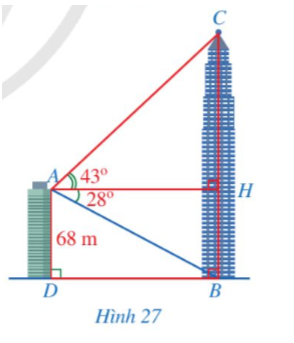
Vì AH ⊥ BC và BD ⊥ BC nên AH // BD. Do đó (so le trong).
Khoảng cách BD từ chân tháp đến chân tòa nhà là:
Do tứ giác ADBH có nên ADBH là hình chữ nhật.
Suy ra AH = DB ≈ 127, 9 (m) và HB = AD = 68 (m).
Do ∆AHC vuông tại H, ta có
Chiều cao BC của tháp truyền hình là: BC = BH + HC ≈ 68 + 119,3 = 187,3 (m).
Vậy khoảng cách BD từ chân tháp đến chân tòa nhà khoảng 127,9 mét và chiều cao BC của tháp truyền hình khoảng 187,3 mét.
Lời giải
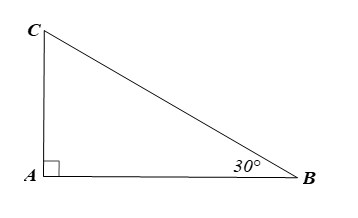
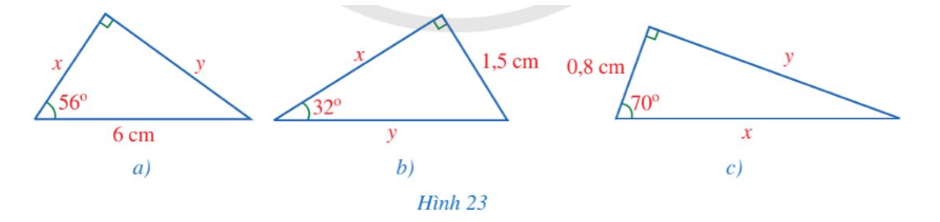
Xét ∆ABC vuông tại A, ta có:
Vậy
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.