Quảng cáo
Trả lời:
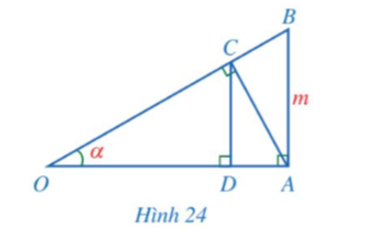
a) Xét ∆OAB vuông tại A, ta có: OA = AB.cotO = m.cotα.
b) Xét ∆OAC vuông tại C, ta có:
(Theo kết quả câu b, Bài 7, SGK Toán 9, Tập 1, trang 81 ta có
c) Xét ∆OAC vuông tại C, ta có:
(Theo kết quả câu b, Bài 7, SGK Toán 9, Tập 1, trang 81 ta có
Xét ∆OCD vuông tại D, ta có:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
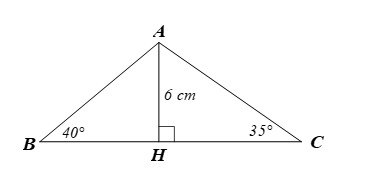
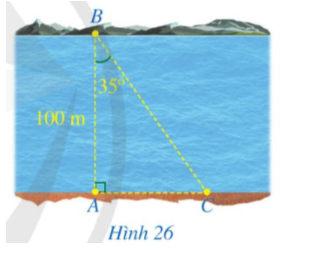
Xét ∆ABH vuông tại H, ta có:
⦁ suy ra
⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).
Xét ∆ACH vuông tại H, ta có:
⦁ suy ra
⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm).
Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm).
Lời giải
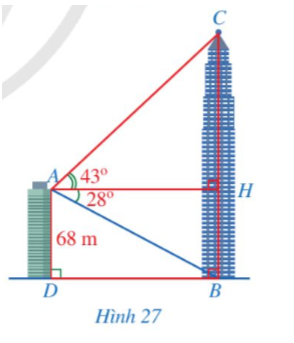
Vì AH ⊥ BC và BD ⊥ BC nên AH // BD. Do đó (so le trong).
Khoảng cách BD từ chân tháp đến chân tòa nhà là:
Do tứ giác ADBH có nên ADBH là hình chữ nhật.
Suy ra AH = DB ≈ 127, 9 (m) và HB = AD = 68 (m).
Do ∆AHC vuông tại H, ta có
Chiều cao BC của tháp truyền hình là: BC = BH + HC ≈ 68 + 119,3 = 187,3 (m).
Vậy khoảng cách BD từ chân tháp đến chân tòa nhà khoảng 127,9 mét và chiều cao BC của tháp truyền hình khoảng 187,3 mét.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.