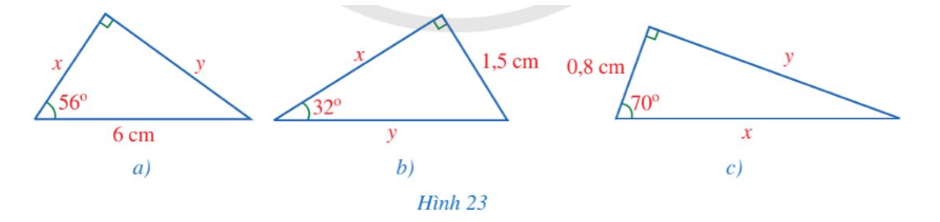
Từ vị trí A ở phía trên một tòa nhà có chiều cao AD = 68 m, bác Duy nhìn thấy vị trí C cao nhất của một tháp truyền hình, góc tạo bởi tia AC và tia AH theo phương nằm ngang là Bác Duy cũng nhìn thấy chân tháp tại vị trí B mà góc tạo bởi tia AB và tia AH là điểm H thuộc đoạn thẳng BC (Hình 27). Tính khoảng cách BD từ chân tháp đến chân tòa nhà và chiều cao BC của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).
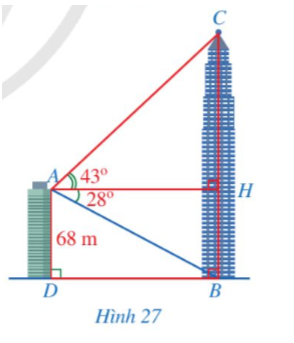
Từ vị trí A ở phía trên một tòa nhà có chiều cao AD = 68 m, bác Duy nhìn thấy vị trí C cao nhất của một tháp truyền hình, góc tạo bởi tia AC và tia AH theo phương nằm ngang là Bác Duy cũng nhìn thấy chân tháp tại vị trí B mà góc tạo bởi tia AB và tia AH là điểm H thuộc đoạn thẳng BC (Hình 27). Tính khoảng cách BD từ chân tháp đến chân tòa nhà và chiều cao BC của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì AH ⊥ BC và BD ⊥ BC nên AH // BD. Do đó (so le trong).
Khoảng cách BD từ chân tháp đến chân tòa nhà là:
Do tứ giác ADBH có nên ADBH là hình chữ nhật.
Suy ra AH = DB ≈ 127, 9 (m) và HB = AD = 68 (m).
Do ∆AHC vuông tại H, ta có
Chiều cao BC của tháp truyền hình là: BC = BH + HC ≈ 68 + 119,3 = 187,3 (m).
Vậy khoảng cách BD từ chân tháp đến chân tòa nhà khoảng 127,9 mét và chiều cao BC của tháp truyền hình khoảng 187,3 mét.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
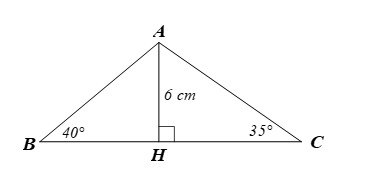
Xét ∆ABH vuông tại H, ta có:
⦁ suy ra
⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).
Xét ∆ACH vuông tại H, ta có:
⦁ suy ra
⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm).
Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm).
Lời giải
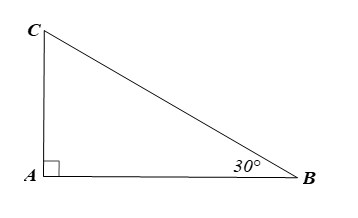
Xét ∆ABC vuông tại A, ta có:
Vậy
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo