Bảng 24 thống kê độ ẩm không khí trung bình các tháng năm 2021 tại Đà Lạt và Vũng Tàu (đơn vị: %).

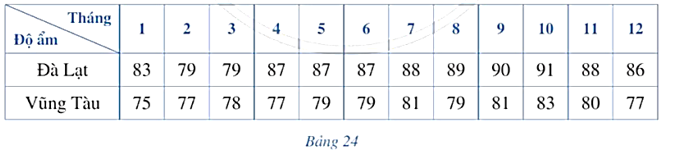
(Nguồn: Niên giám Thống kê 2021, NXB Thống kê, 2022)

a) Hãy lần lượt ghép các số liệu của Đà Lạt, Vũng Tàu thành năm nhóm sau:

[75; 78,3), [78,3; 81,6), [81,6; 84,9), [84,9; 88,2), [88,2; 91,5).

 Hà Nội

Ÿ Trong mẫu số liệu ghép nhóm ở Bảng 22, ta có: đầu mút trái của nhóm 1 là a₁ = 16,8; đầu mút phải của nhóm 5 là a₆ = 31,8.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:

R = a₆ – a₁ = 31,8 – 16,8 = 15 (độ C).

ŸTừ Bảng 22 ta có bảng thống kê sau:

Số phần tử của mẫu là n = 12.

- Ta có:  $\frac{n}{4}=\frac{12}{4}=3$ mà 2 < 3 < 5. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 2 là nhóm [19,8; 22,8) có s = 19,8; h = 3; n₂ = 3 và nhóm 1 là nhóm [16,8; 19,8) có cf₁ = 2.

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

 ${Q^{\text{'}}}_1=19,8+\left(\frac{3-1}{2}\right)\cdot 3=22,8$ (độ C).

- Ta có:  $\frac{3n}{4}=\frac{3\cdot 12}{4}=9$ mà 8 < 9 < 12. Suy ra nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 5 là nhóm [28,8; 31,8) có t = 28,8; l = 3; n₅ = 4 và nhóm 4 là nhóm [25,8; 28,8) có cf₄ = 8.

Áp dụng công thức, ta có tứ phân vị thứ ba là:

 ${Q^{\text{'}}}_3=28,8+\left(\frac{9-8}{4}\right)\cdot 3=29,55$ (độ C).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:  

∆_Q = Q₃ – Q₁ = 29,55 – 20,8 = 8,75 (độ C).

Ÿ Số trung bình cộng của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:

 $\overline{x^{\text{'}}}=\frac{1\cdot 18,3+2\cdot 21,3+3\cdot 24,3+2\cdot 27,3+4\cdot 30,3}{12}=\frac{309,6}{12}=25,8$ (độ C).

Vậy phương sai của của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:

 ${s^{\text{'}}}^2=\frac{1}{12}$∙ [2 ∙ (18,3 – 24,8)² + 3 ∙ (21,3 – 24,8)² + 2 ∙ (24,3 – 24,8)²

                     + 1 ∙ (27,3 – 24,8)² + 4 ∙ (30,3 – 24,8)²] =   $\frac{249}{12}$ = 20,75.

Ÿ Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là:  $s=\sqrt{20,75}\approx 4,56$ (độ C).

‚ Huế

Ÿ Trong mẫu số liệu ghép nhóm ở Bảng 23, ta có: đầu mút trái của nhóm 1 là a₁ = 16,8; đầu mút phải của nhóm 5 là a₆ = 31,8.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:

R' = a₆ – a₁ = 31,8 – 16,8 = 15 (độ C).

ŸTừ Bảng 23 ta có bảng thống kê sau:

Số phần tử của mẫu là n = 12.

- Ta có:  $\frac{n}{4}=\frac{12}{4}=3$ mà 1 < 3. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 2 là nhóm [19,8; 22,8) có s = 19,8; h = 3; n₂ = 2 và nhóm 1 là nhóm [16,8; 19,8) có cf₁ = 1.

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

 ${Q^{\text{'}}}_1=19,8+\left(\frac{3-1}{2}\right)\cdot 3=22,8$ (độ C).

- Ta có:  $\frac{3n}{4}=\frac{3\cdot 12}{4}=9$ mà 8 < 9 < 12. Suy ra nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 5 là nhóm [28,8; 31,8) có t = 28,8; l = 3; n₅ = 4 và nhóm 4 là nhóm [25,8; 28,8) có cf₄ = 8.

Áp dụng công thức, ta có tứ phân vị thứ ba là:

 ${Q^{\text{'}}}_3=28,8+\left(\frac{9-8}{4}\right)\cdot 3=29,55$ (độ C).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:

∆'_Q = Q'₃ – Q'₁ = 29,55 – 22,8 = 6,75 (độ C).

Ÿ Số trung bình cộng của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:

 $\overline{x^{\text{'}}}=\frac{1\cdot 18,3+2\cdot 21,3+3\cdot 24,3+2\cdot 27,3+4\cdot 30,3}{12}=\frac{309,6}{12}=25,8$ (độ C).

Vậy phương sai của của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:

 ${s^{\text{'}}}^2=\frac{1}{12}$∙ [1 ∙ (18,3 – 25,8)² + 2 ∙ (21,3 – 25,8)² + 3 ∙ (24,3 – 25,8)²

                     + 2 ∙ (27,3 – 25,8)² + 4 ∙ (30,3 – 25,8)²] =  $\frac{189}{12}$ = 15,75.

Ÿ Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là:  $s^{\text{'}}=\sqrt{15,75}\approx 3,97$ (độ C).

Đáp án đúng là: C

Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó là ∆_Q = Q₃ – Q₁.