Giải SGK Toán 12 Cánh diều Bài tập cuối Chương III có đáp án
32 người thi tuần này 4.6 451 lượt thi 6 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: C
Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó là ∆Q = Q3 – Q1.
Lời giải
Hà Nội
Trong mẫu số liệu ghép nhóm ở Bảng 22, ta có: đầu mút trái của nhóm 1 là a1 = 16,8; đầu mút phải của nhóm 5 là a6 = 31,8.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:
R = a6 – a1 = 31,8 – 16,8 = 15 (độ C).
Từ Bảng 22 ta có bảng thống kê sau:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[16,8; 19,8) |
2 |
2 |
|
[19,8; 22,8) |
3 |
5 |
|
[22,8; 25,8) |
2 |
7 |
|
[25,8; 28,8) |
1 |
8 |
|
[28,8; 31,8) |
4 |
12 |
|
|
n = 12 |
|
Số phần tử của mẫu là n = 12.
- Ta có: mà 2 < 3 < 5. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 2 là nhóm [19,8; 22,8) có s = 19,8; h = 3; n2 = 3 và nhóm 1 là nhóm [16,8; 19,8) có cf1 = 2.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(độ C).
- Ta có: mà 8 < 9 < 12. Suy ra nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 5 là nhóm [28,8; 31,8) có t = 28,8; l = 3; n5 = 4 và nhóm 4 là nhóm [25,8; 28,8) có cf4 = 8.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(độ C).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:
∆Q = Q3 – Q1 = 29,55 – 20,8 = 8,75 (độ C).
Số trung bình cộng của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:
(độ C).
Vậy phương sai của của mẫu số liệu ghép nhóm được cho bởi Bảng 22 là:
∙ [2 ∙ (18,3 – 24,8)2 + 3 ∙ (21,3 – 24,8)2 + 2 ∙ (24,3 – 24,8)2
+ 1 ∙ (27,3 – 24,8)2 + 4 ∙ (30,3 – 24,8)2] = = 20,75.
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: (độ C).
Huế
Trong mẫu số liệu ghép nhóm ở Bảng 23, ta có: đầu mút trái của nhóm 1 là a1 = 16,8; đầu mút phải của nhóm 5 là a6 = 31,8.
Vậy khoảng biến thiên của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:
R' = a6 – a1 = 31,8 – 16,8 = 15 (độ C).
Từ Bảng 23 ta có bảng thống kê sau:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[16,8; 19,8) |
1 |
1 |
|
[19,8; 22,8) |
2 |
3 |
|
[22,8; 25,8) |
3 |
6 |
|
[25,8; 28,8) |
2 |
8 |
|
[28,8; 31,8) |
4 |
12 |
|
|
n = 12 |
|
Số phần tử của mẫu là n = 12.
- Ta có: mà 1 < 3. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 2 là nhóm [19,8; 22,8) có s = 19,8; h = 3; n2 = 2 và nhóm 1 là nhóm [16,8; 19,8) có cf1 = 1.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(độ C).
- Ta có: mà 8 < 9 < 12. Suy ra nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 5 là nhóm [28,8; 31,8) có t = 28,8; l = 3; n5 = 4 và nhóm 4 là nhóm [25,8; 28,8) có cf4 = 8.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(độ C).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:
∆'Q = Q'3 – Q'1 = 29,55 – 22,8 = 6,75 (độ C).
Số trung bình cộng của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:
(độ C).
Vậy phương sai của của mẫu số liệu ghép nhóm được cho bởi Bảng 23 là:
∙ [1 ∙ (18,3 – 25,8)2 + 2 ∙ (21,3 – 25,8)2 + 3 ∙ (24,3 – 25,8)2
+ 2 ∙ (27,3 – 25,8)2 + 4 ∙ (30,3 – 25,8)2] = = 15,75.
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: (độ C).
Lời giải
b) Vì s' ≈ 3,97 < s ≈ 4,56 nên thành phố Huế có nhiệt độ không khí trung bình tháng đồng đều hơn thành phố Hà Nội.
Lời giải
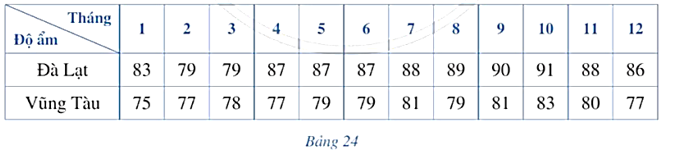
a) Từ Bảng 24, ta có các bảng thống kê sau:
|
Nhóm |
Giá trị đại diện |
Tần số |
|
Nhóm |
Giá trị đại diện |
Tần số |
|
[75; 78,3) |
76,65 |
0 |
|
[75; 78,3) |
76,65 |
5 |
|
[78,3; 81,6) |
79,95 |
2 |
|
[78,3; 81,6) |
79,95 |
6 |
|
[81,6; 84,9) |
83,25 |
1 |
|
[81,6; 84,9) |
83,25 |
1 |
|
[84,9; 88,2) |
86,55 |
7 |
|
[84,9; 88,2) |
86,55 |
0 |
|
[88,2; 91,5) |
89,85 |
2 |
|
[88,2; 91,5) |
89,85 |
0 |
|
|
|
n = 12 |
|
|
|
n = 12 |
Đà Lạt Vũng Tàu
Lời giải
b)
Đà Lạt
Khoảng biến thiên của mẫu số liệu ghép nhóm của Đà Lạt là:
R = 91,5 – 78,3 = 13,2 (%).
Từ bảng thống kê trên, ta có bảng thống kê của mẫu số liệu ghép nhóm của Đà Lạt:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[78,3; 81,6) |
2 |
2 |
|
[81,6; 84,9) |
1 |
3 |
|
[84,9; 88,2) |
7 |
10 |
|
[88,2; 91,5) |
2 |
12 |
|
|
n = 12 |
|
Số phần tử của mẫu là n = 12.
- Ta có: mà 2 < 3. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 2 là nhóm [81,6; 84,9) có s = 81,6; h = 3,3; n2 = 1 và nhóm 1 là nhóm [78,3; 81,6) có cf1 = 2.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(%).
- Ta có: mà 3 < 9 < 10. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 3 là nhóm [84,9; 88,2) có t = 84,9; l = 3,3; n3 = 7 và nhóm 2 là nhóm [81,6; 84,9) có cf2 = 3.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(%).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm của Đà Lạt là:
∆Q = Q3 – Q1 = 87,7 – 84,9 = 2,8 (%).
Số trung bình cộng của mẫu số liệu ghép nhóm của Đà Lạt là:
(%).
Vậy phương sai của của mẫu số liệu ghép nhóm của Đà Lạt là:
∙ [2 ∙ (79,95 – 85,725)2 + 1 ∙ (83,25 – 85,725)2 + 7 ∙ (86,55 – 85,725)2
+ 2 ∙ (89,85 – 85,725)2] = ≈ 9,3.
Độ lệch chuẩn của mẫu số liệu ghép nhóm của Đà Lạt là: (%).
Vũng Tàu
Khoảng biến thiên của mẫu số liệu ghép nhóm của Vũng Tàu là:
R' = 84,9 – 75 = 9,9 (%).
Từ bảng thống kê trên, ta có bảng thống kê của mẫu số liệu ghép nhóm của Vũng Tàu:
|
Nhóm |
Tần số |
Tần số tích lũy |
|
[75; 78,3) |
5 |
5 |
|
[78,3; 81,6) |
6 |
11 |
|
[81,6; 84,9) |
1 |
12 |
|
|
n = 12 |
|
Số phần tử của mẫu là n = 12.
- Ta có: mà 5 > 3. Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3. Xét nhóm 1 là nhóm [75; 78,3) có s = 75; h = 3,3; n1 = 5.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
(%).
- Ta có: mà 5 < 9 < 11. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Xét nhóm 2 là nhóm [78,3; 81,6) có t = 78,3; l = 3,3; n2 = 6 và nhóm 1 là nhóm [75; 78,3) có cf1 = 5.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
(%).
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm của Vũng Tàu là:
∆'Q = Q'3 – Q'1 = 80,5 – 76,98 = 3,52 (%).
Số trung bình cộng của mẫu số liệu ghép nhóm của Vũng Tàu là:
(%).
Vậy phương sai của của mẫu số liệu ghép nhóm của Vũng Tàu là:
∙ [5 ∙ (76,65 – 78,85)2 + 6 ∙ (79,95 – 78,85)2 + 1 ∙ (83,25 – 78,85)2]
= = 4,235.
Độ lệch chuẩn của mẫu số liệu ghép nhóm của Vũng Tàu là: (%).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.